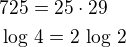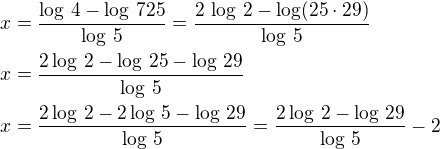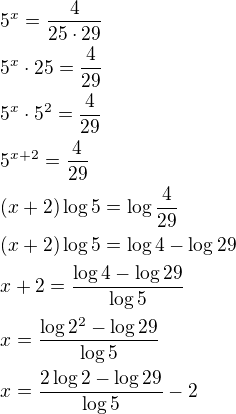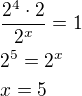Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 09. 06. 2010 09:47
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
exponenciální rovnice 3.
Ahoj, mohl by mě někdo pomoc s tímto příkladem? Strašně moc děkuji.
Offline
- (téma jako vyřešené označil(a) Lucinecka88)
#2 09. 06. 2010 09:59
Re: exponenciální rovnice 3.
↑ Lucinecka88:
Ahoj. Jak sleduju tvoje příspěvky, nemůžu se ubránit dojmu, že ty příklady jsou všechny stejné, a že by neuškodilo trochu vlastní invence.
Tady bych asi doporučoval převést si trojku na jednu stranu, rovnici zlogaritmovat (obě strany jsou kladné) a pak chvíli upravovat, dokud něco nevyjde. Zkus poslat svůj postup.
Offline
#3 09. 06. 2010 10:00
- teolog


- Místo: Praha
- Příspěvky: 3497
- Škola: MFF + PřF UK
- Pozice: Gymnázium Přírodní škola - učitel (M, Z)
- Reputace: 167
Re: exponenciální rovnice 3.
↑ Lucinecka88: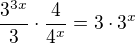 vynásobíme rovnici 3*4^x
vynásobíme rovnici 3*4^x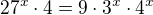
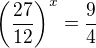
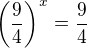

Offline
#4 09. 06. 2010 10:22
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: exponenciální rovnice 3.
↑ LukasM:
Už ho mám. Vím že jsou na jedno brdo,ale já opravdu nevím jak mám začít.
Offline
#5 09. 06. 2010 11:43 — Editoval Lucinecka88 (09. 06. 2010 11:44)
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: exponenciální rovnice 3.
Můžete mi to někdo prosím zkontrolovat? Pokud to mám dobře tak co mám dál dělat? Pokud ne tak kde mám chybu?
Offline
#6 09. 06. 2010 12:21 — Editoval Cheop (09. 06. 2010 12:21)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: exponenciální rovnice 3.
↑ Lucinecka88:
Úprava je dobře, ale je potřeba to dopočítat: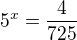 zlogaritmovat a dostaneme:
zlogaritmovat a dostaneme: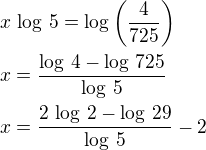
Nikdo není dokonalý
Offline
#7 09. 06. 2010 13:01
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: exponenciální rovnice 3.
↑ Cheop:
Proč máš u posledního řádku -2 a jak jsi přišel na 29?
Offline
#8 09. 06. 2010 13:10
#10 09. 06. 2010 14:03
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: exponenciální rovnice 3.
Mohl by mě prosím někdo říct co děláš špatně? Nevím jak mám pokračovat. Děkuji
Offline
#11 09. 06. 2010 14:11 — Editoval stepan.machacek (09. 06. 2010 14:12)
- teolog


- Místo: Praha
- Příspěvky: 3497
- Škola: MFF + PřF UK
- Pozice: Gymnázium Přírodní škola - učitel (M, Z)
- Reputace: 167
Re: exponenciální rovnice 3.
↑ Lucinecka88:
Já osobně bych nejprve upravil mocniny typu 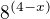 na
na 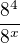 a to v celé rovnici.
a to v celé rovnici.
Offline
#12 09. 06. 2010 14:13
Re: exponenciální rovnice 3.
↑ Lucinecka88:
Chyba tam zatím není, ale je třeba pokračovat dalšími úpravami, v nichž příjdou ke slovu vzorce
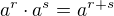 ,
, 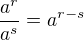 .
.
Offline
#13 09. 06. 2010 14:14
Re: exponenciální rovnice 3.
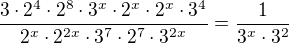
a můžeš pokračovat, musím vytáhnout bábovku z trouby... :)
(všechny kladné exponenty jsou v čitateli, všechny záporné ve jmenovateli a naopak...)
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline