Matematické Fórum

Lucinecka88 · 09. 06. 2010 15:51

Prosím o pomoc. Nevím si rady u těchto příkladů, ani nevím jak mám začít. Děkuji

hradecek

↑ Lucinecka88:
1.)Logaritmujem:
$x^{2+log_2(x)}=8\nl log_2(x)^{2+log_2(x)}=log_2(8)\nl (2+log_2x)(log_2x)=log_2(8)\nl subs:\quad t=log_2(x)\nl t^2+2t-3=0$
Vyriešiš kvadratickú rovnicu dosadíš do substitúcie a prídeš k výsledkom:

Autor skryl část textu. Zobrazit/skrýt!

nezabudni na podmienky...

Lucinecka88 · 09. 06. 2010 16:57

↑ hradecek:

Děkuji. A co mám udělat s těmi dalšími?

gadgetka · 09. 06. 2010 17:00

2)
$\log_3 x=a \Rightarrow x=3^a$

$(3^{a})^{\frac{a}{5}}=3^5\nl\frac{a^2}{5}=5\nla^2=25\nla=\pm 5$

$x_1=3^{5}\nlx_2=\frac{1}{3^5}$

gadgetka

3)
$s: x^{\log x}=a\nla+\frac{10}{a}=11\nla^2+10=11a\nla^2-11a+10=0\nla_{1,2}=\frac{11\pm 9}{2}\nla_1=10\nla_2=1\nlx^{\log x}=10\nlx_1=10\nlx_2=\frac{1}{10}\nlx^{\log x}=1\nlx_3=1$

Lucinecka88

↑ gadgetka:

Děkuji. U té dvojky bych potřebovala podrobněji vysvětlit, tak aby mě to uznala učitelka. U té trojky jsi zjistila jak ty x?

gadgetka · 09. 06. 2010 17:49

2)
je to substituce, 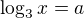$\log_3 x=a$

A když je 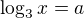$\log_3 x=a$ , tak podle pravidel počítání s logaritmy platí, že $3^a=x$

tak6e pod odmocninou máme $(3^a)^a$ , je to pátá odmocnina, čili celý výraz pod odmocninou umocníme na $\frac{1}{5}$ a dostaneme $(3^{a^2})^{\frac{1}{5}}$ , což je $3^{\frac{a^2}{5}}$ . Na pravé straně je $243$ , což je $3^5$ . Zbytek určitě chápeš.