Matematické Fórum

Kendy · 10. 06. 2010 19:34

Prosím o pomoc, výpočty takovýchto úloh je pro mne peklo. :(
1) Vypočítejte povrch a objem pravidelného čtyřbokého jehlanu. Úhlopříčka je 8,5 cm. Výška je 5 cm.
2)Vypočítejte objem rotačního kužele, je-li obvod jeho podstavy 69 cm a strana má délku 15 cm.
3)Kolik dm2 kůže je třeba na výrobu míče, jehož obvod je 78,5 cm? Na sešití počítejte 6% materiálu.

Tyhle tři z deseti mi nevycházejí, u toho prvního jsem na to šla přes pythagorovu větu, ale nepochodila jsem. U dalších nemám ani zdání jak na to. Děkuji předem za pomoc. :)

Kendy · 10. 06. 2010 19:35

Jej, velice se omlouvám za vložení tří úloh do jednoho tématu. Zapomněla jsem, že se to nesmí.

Ivana · 10. 06. 2010 19:54

↑ Kendy:

1. Návod k řešení :

byk7 · 10. 06. 2010 19:59

↑ Kendy:

[1]
stranu čtverce spočítáš z Pythagorovy věty: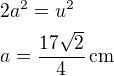
$2a^2=u^2 \nl a=\frac{17\sqrt2}{4}\,\rm{cm}$
$V=\frac{1}{3}a^2v=\frac{1}{3}\cdot$\frac{17\sqrt2}{4}$\cdot5$
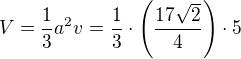
dopočítáš

[2]
vypočítej poloměr: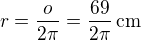
$r=\frac{o}{2\pi}=\frac{69}{2\pi}\,\rm{cm}$
a výšku z Pythagorovy věty: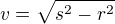
$v=\sqrt{s^2-r^2}$
a nakonec objem: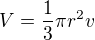
$V=\frac{1}{3}\pi r^2v$

[3]
asi se myslí maximální obvod, že?
opět vypočítáš poloměr: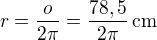
$r=\frac{o}{2\pi}=\frac{78,5}{2\pi}\,\rm{cm}$
vypočítáš povrch: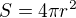
$S=4\pi r^2$
a vypočítáš 106%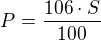
$P=\frac{106\cdot S}{100}$
(P je spotřeba materiálu)