Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 10. 06. 2010 18:58
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Systém diferenciálnych rovníc
Prosím, poraďte mi ako vyriešiť tento systém troch dif. rovníc (počiatočné podmienky nemám zadané):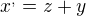
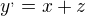
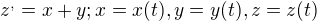
Riešenie má byť v tvare 3 rovníc, pre každú funkciu jedna, no medzi konštantami v jednotlivých rovniciach je nejaký vzťah, a tak miesto pôvodných 9 mám použiť len 3, riešenie by vraj malo vyzerať nejak takto: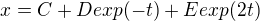
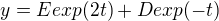
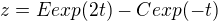
Dpracoval som sa k rieseniu pre x (prva rovnica), no neviem ako ďalej postupovať aby som našiel vzťahy medzi konštantami.
Offline
#2 10. 06. 2010 19:26
- kaja(z_hajovny)

- Místo: Lážov
- Příspěvky: 1002
- Reputace: 12
- Web
Re: Systém diferenciálnych rovníc
A mate vypocitana vlastni cisla a vlastni vektory? Sem s nimi :)
Offline
#4 10. 06. 2010 19:42
Re: Systém diferenciálnych rovníc
↑ Ferdish: pozdravujem a posielam.... najpohodlnejsie to sa da Laplaceom..a skuska vysla
Offline
#5 10. 06. 2010 19:45
- kaja(z_hajovny)

- Místo: Lážov
- Příspěvky: 1002
- Reputace: 12
- Web
Re: Systém diferenciálnych rovníc
↑ Ferdish:
tak sem dejte Vase reseni. Anebo tim Laplacem :)
Offline
#6 10. 06. 2010 20:11
- Ferdish

- Zablokovaný
- Příspěvky: 4173
- Škola: PF UPJŠ (2013), ÚEF SAV (2017)
- Pozice: vedecký pracovník
- Reputace: 81
Re: Systém diferenciálnych rovníc
Nikde som nenapísal že som úlohu vyriešil. To že poznám jej výsledok nie je priamym dôkazom...
Moje riešenie:
x' = y + z (derivujem)
x'' = y' + z' (dosadim za derivacie z druhej a tretej rovnice)
x'' = 2x + y + z = 2x + x' (opat derivujem)
x''' - x'' - 2x' = 0
Riešim homogennu rovnicu, a dospejem k riešeniu pre x napísanom vyššie.
A teraz ako zistiť riešenie pre ostatné 2 rovnice. Keby bola len jedna, nie je problém vyjadriť fciu y ako funkciu od čisto od x. To ale v tomto prípade nemôžem spraviť, preto sa pýtam ako na to. Dík.
Offline
#7 10. 06. 2010 20:20
- kaja(z_hajovny)

- Místo: Lážov
- Příspěvky: 1002
- Reputace: 12
- Web
Re: Systém diferenciálnych rovníc
No nejak jsem myslel, ze Vam odnekud vyslo devet konstant. Nevedel jsem, ze to byly virtualni konstanty :)
x' = y + z odsud vyjadrim z a dosadim do x'' = 2x + y + z = 2x + x' , v rovnici bude x, x', x'' a y, y vypocitam
Offline
#9 10. 06. 2010 21:06
- kaja(z_hajovny)

- Místo: Lážov
- Příspěvky: 1002
- Reputace: 12
- Web
Re: Systém diferenciálnych rovníc
hm to je pravda, tak treba nejak podobne
Offline
 x'' = 2x + y + x' - y = 2x + x'.
x'' = 2x + y + x' - y = 2x + x'.