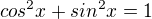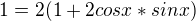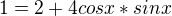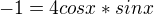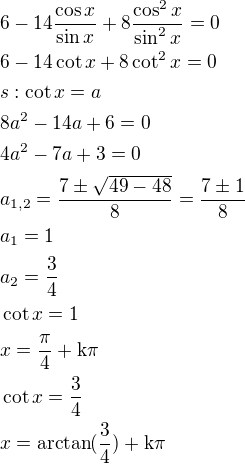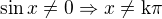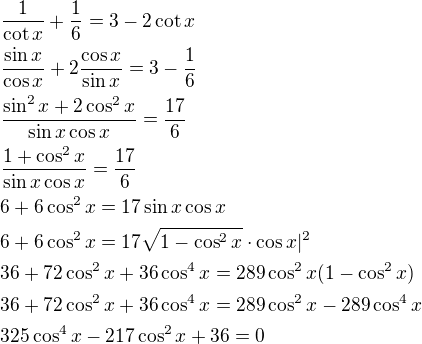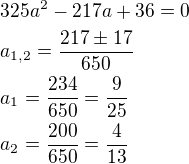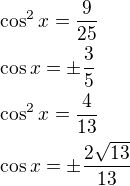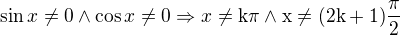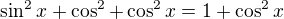Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Střední škola
- » goniometrické rovnice 3. (poslední) (TOTO TÉMA JE VYŘEŠENÉ)
#1 11. 06. 2010 08:20
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
goniometrické rovnice 3. (poslední)
Prosím o pomoc s těmito příklady. Nevím si rady a ani sestra mi nepomohla. Strašně moc děkuji za pomoc.
Offline
- (téma jako vyřešené označil(a) Lucinecka88)
#2 11. 06. 2010 08:53 — Editoval kacka18 (11. 06. 2010 08:59)
Re: goniometrické rovnice 3. (poslední)
zatím mám 3.):
odstraníš jmenovatele vynásobením rce 6*cotgx
vyjde rce: 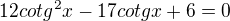
substituce: 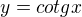
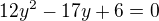
kořeny kvadratické rce: 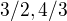
Vrátíš do substituce a vyšlo mi 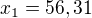 a
a 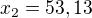
Snad je to správně, nemám moc čas to kontrolovat :) Postup by měl být správně.
Offline
#5 11. 06. 2010 09:22
#6 11. 06. 2010 09:38
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: goniometrické rovnice 3. (poslední)
Zdravím vás a děkuji za řešení.
Jen takové drobnosti:
- provádění neekvivalentních úprav (dělení výrazem s promennou) je bez poznámky o podmínce, za které může být tato úprava provedena. V postupu pro 4) řekla bych, že dokonce takovou úpravou bylo jedno řešení ztraceno. Je to tak? Děkuji.
Vlastní snaha ↑ Lucinecky88: (co jsem nakoukla do dalších témat) je bohužel minimální a pochybuji, že se snaží vytvořit systém v jednotlivých postupech. Zřejmě to není účelem.
Ať se vede.
Offline
#8 11. 06. 2010 09:54
Re: goniometrické rovnice 3. (poslední)
↑ jelena:
Zdravím ... a jen doplňuji, že Lucinečku jsem již jednou na podmínky upozorňovala, takže jsem to vzala tak, že to už je na ní ... jinak souhlasím s tebou v tom, že Lucinečka má bez nějakého většího přičinění komplet "zvládnutou" látku o goniometrických rovnicích...
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#9 11. 06. 2010 11:04
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: goniometrické rovnice 3. (poslední)
↑ gadgetka:
děkuji, ovšem zde není individuální prostor pro výcvik Lucinečky, na toto řešení se může podívat někdo další a bude se divit. Nebo nebude a zafixuje si neúplný postup. Navíc si myslím, že v 4) došlo ke ztratě části kořenu.
Ovšem v tématech SŠ se velmi těžce reaguje - o nějakém prosazování pravidel - body 2, 4 - nelze ani mluvit. Pokud se to nedodržuje ze strany účastníku tématu... ale to je úplně OT ve vztahu k tématu, tedy konec OT, případně se to může řešit v Připominkach
Offline
#10 11. 06. 2010 11:39 — Editoval Rumburak (11. 06. 2010 11:42)
Re: goniometrické rovnice 3. (poslední)
↑ jelena:
Souhlas, v příspěvku ↑ kacka18: ze ztratila ta řešení původní rovnice, která jsou zároveň řešeními rovnice 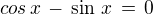 .
.
kacka18 napsal(a):
.
.
.
Závorkase vykrátí a zbyde:
Offline
#11 11. 06. 2010 15:35
Re: goniometrické rovnice 3. (poslední)
↑ Rumburak:
jj, nesmí se to krátit, musí se to vytýkat ...
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#12 14. 06. 2010 09:58
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: goniometrické rovnice 3. (poslední)
Ahoj, omlouvám se, že to vypadá, jako kdybych chtěla spočítat všechny příklady po vás, ale mám zhruba 300 příkladů ke každýmu tématu a dávám sem příklady jen ty, s kterými si opravdu nevím rady. Vím, že nejsem silná matematička, ale snažím se udělat co nejvíc umím. Mockrát všem děkuji za pomoc, kterou jste mi tu zatím poskytli a byla bych strašně moc vděčná, kdybyste mi mohli pomáhat dál.
Offline
#13 14. 06. 2010 14:00
Re: goniometrické rovnice 3. (poslední)
Ještě jednou, aby to Lucinečka lépe pochopila:
2)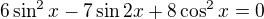
Pomocné výpočty: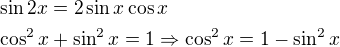
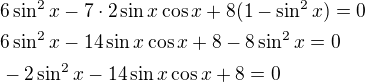
Pomocné výpočty: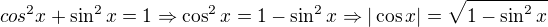
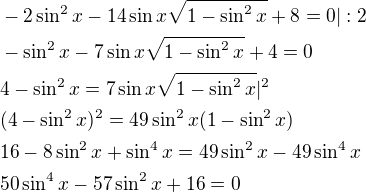
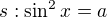
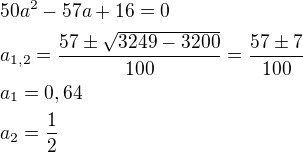
Dosadíme zpět do substituce: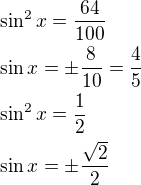
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#15 14. 06. 2010 19:10
Re: goniometrické rovnice 3. (poslední)
4)
1. 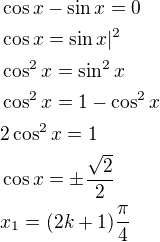
nebo
2.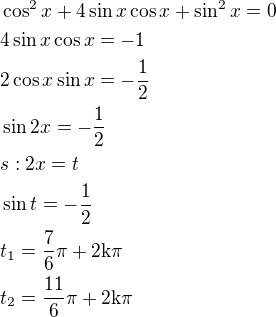
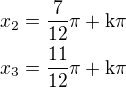
Podmínky: 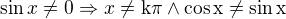
U 1. řešení můžeš i vypsat všechna řešení, pro všechny 4 kvadranty, obojí je správně
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#16 14. 06. 2010 22:38
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: goniometrické rovnice 3. (poslední)
↑ gadgetka:
Prosím tě, můžu se zeptat jak jsi udělala z 3 řádku 4 řádek u příkladu 3? Děkuji
Offline
#18 14. 06. 2010 23:02
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: goniometrické rovnice 3. (poslední)
A jo, děkuju.
Offline
#20 15. 06. 2010 11:33
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: goniometrické rovnice 3. (poslední)
Děkuji za pomoc
Offline
Stránky: 1
- Hlavní strana
- » Střední škola
- » goniometrické rovnice 3. (poslední) (TOTO TÉMA JE VYŘEŠENÉ)
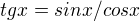
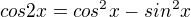
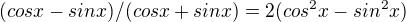 ... pravá strana je vzoreček
... pravá strana je vzoreček 
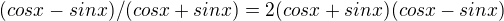
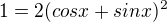
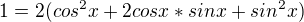 ...
...