Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 09. 06. 2010 23:10
délka křivky..deltadelta
http://upload.wikimedia.org/math/e/2/e/ … 9aac00.png
čtu si to pořád dokola.. ale prostě mi nedochází ten druhej krok..
jak ze závorky  mohli vytknout
mohli vytknout 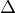 a dostat
a dostat 
prosím o nakopnutí.. asi sem zas dlouho nedělal matiku :-)
(: SMILE :)
Offline
- (téma jako vyřešené označil(a) graviton)


 ..
..