Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 12. 06. 2010 19:08 — Editoval lucik.kicul (12. 06. 2010 19:22)
- lucik.kicul
- Příspěvky: 126
- Reputace: 0
goniometrie
Potřebovala bych pomoci s goniometrickými příklady, goniometrie totiž není moje silná stránka,
ráda bych kdyby jste mi u těchto ukázkových příkladů poradili s postupem, pro mě prosím jednodušeji,
1.počet všech x \in (0,pí), pro která platí cos x=5/7, je roven číslu: výsledek má vyjít 1
2.počet všech x \in <pí/3,2pí>, pro která platí 2cos^2x=cos x, je roven číslu: výsledek 4
3.počet všech x \in <0,pí), pro která platí 2cos^2x=\sprt 2 cosx, je roven číslu: výsledek 2
4. počet všech x \in (0,pí), pro která platí sinx=-2/3, je roven číslu: výsledek 0
chápu u tohoto příkladu dobře, že když je mínus, tak se vždy rovná 0?
děkuju moc
Offline
- (téma jako vyřešené označil(a) gadgetka)
#2 12. 06. 2010 19:32
- lucik.kicul
- Příspěvky: 126
- Reputace: 0
Re: goniometrie
Potřebovala bych pomoci s goniometrickými příklady, goniometrie totiž není moje silná stránka,
ráda bych kdyby jste mi u těchto ukázkových příkladů poradili s postupem, pro mě prosím jednodušeji,
1.počet všech x \in (0,pí), pro která platí cos x=5/7, je roven číslu: výsledek má vyjít 1
2.počet všech x \in <pí/3,2pí>, pro která platí 2cos^2x=cos x, je roven číslu: výsledek 4
3.počet všech x \in <0,pí), pro která platí 2cos^2x=\sprt 2 cosx, je roven číslu: výsledek 2
4. počet všech x \in (0,pí), pro která platí sinx=-2/3, je roven číslu: výsledek 0
chápu u tohoto příkladu dobře, že když je mínus, tak se vždy rovná 0?
děkuju moc
Offline
#3 12. 06. 2010 19:59
Re: goniometrie
↑ lucik.kicul:
Tu je potrebné si všímať znamienka: znamienko u 5/7 je +, pri funckii kosínus sa nachádzame v I. a IV. kvadrante, ale kedže x môže byť iba z I. a II. tak je možné iba jedno riešenie
znamienko u 5/7 je +, pri funckii kosínus sa nachádzame v I. a IV. kvadrante, ale kedže x môže byť iba z I. a II. tak je možné iba jedno riešenie
Netrápte sa nad svojimi problémami s matematikou, môžem vás uistiť, že tie moje sú ešte väčšie. ~~Albert Einstein~~
Jak spozná člověk, že není pitomec ? - Moudrý člověk to nepozná nikdy a blbci je to jedno. ~~Jak přicházejí básnici o iluze~~
Někteří lidi se nikdy nezmění. Anebo se rychle změní a pak se zase rychle změní nazpátek. ~~Homer Simpson~~
Offline
#5 12. 06. 2010 20:15
- lucik.kicul
- Příspěvky: 126
- Reputace: 0
Re: goniometrie
mám tedy počítat s pomocí kvadrantů?
moc to ještě nechápu
Offline
#6 12. 06. 2010 20:19
- lucik.kicul
- Příspěvky: 126
- Reputace: 0
Re: goniometrie
↑ gadgetka:
u toho druhého příkladu můžu se prosím Vás zeptat, jak přijdu na cos x (2cosx-1)?jinak děkuji =)
Offline
#8 12. 06. 2010 20:21
Re: goniometrie
lucik.kicul napsal(a):
↑ gadgetka:
u toho druhého příkladu můžu se prosím Vás zeptat, jak přijdu na cos x (2cosx-1)?jinak děkuji =)
Převedením na jednu stranu a vytknutím 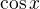
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#9 12. 06. 2010 20:22
- lucik.kicul
- Příspěvky: 126
- Reputace: 0
Re: goniometrie
↑ lucik.kicul:
už jsem si všimla,vytknu si tedy cos x a jak přijdu ke cosx=1/2?
Offline
#10 12. 06. 2010 20:22
Re: goniometrie
lucik.kicul napsal(a):
mám tedy počítat s pomocí kvadrantů?
moc to ještě nechápu
Musíš brát v potaz jen ta řešení, která spadají do příslušného, v zadání uvedeného, kvadrantu.
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#11 12. 06. 2010 20:25
Re: goniometrie
lucik.kicul napsal(a):
↑ lucik.kicul:
už jsem si všimla,vytknu si tedy cos x a jak přijdu ke cosx=1/2?
Když je součin roven nule, platí, že buď jeden nebo druhý činitel musí být roven nule, takže platí: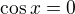 nebo
nebo 
Úpravou druhé rovnice dojdeš k tomu, že 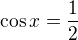
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#12 12. 06. 2010 20:26
- lucik.kicul
- Příspěvky: 126
- Reputace: 0
Re: goniometrie
jj, už mi to došlo, trošku pozdě, ale přeci =), děkuju a můžu se prosím zeptat ještě na ten 4 příklad?
Offline
#13 12. 06. 2010 20:28
Re: goniometrie
4)
Fce sin je záporná ve III. a IV. kvadrantu, ale ty máš řešit I. a II. kvadrant, takže je hned jasné že řešením bude prázdná množina, čili 0 řešení.
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#14 12. 06. 2010 20:39
- lucik.kicul
- Příspěvky: 126
- Reputace: 0
Re: goniometrie
↑ gadgetka:
za všechno moc děkuji, moc jste mi pomohla =)
Offline
#17 12. 06. 2010 21:33
Re: goniometrie
↑ lucik.kicul:
Fce cos x je kladná v I. a IV. kvadrantu, tzn., že kořenem rovnice 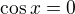 bude jednak
bude jednak  a jednak
a jednak 
Stejně tak u druhé rovnice.
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline







 od 0 až po
od 0 až po 
