Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Plosny obsah casti roviny 4 (TOTO TÉMA JE VYŘEŠENÉ)
#7 09. 06. 2010 21:57 — Editoval stepan.machacek (09. 06. 2010 21:58)
- teolog


- Místo: Praha
- Příspěvky: 3498
- Škola: MFF + PřF UK
- Pozice: Gymnázium Přírodní škola - učitel (M, Z)
- Reputace: 167
Re: Plosny obsah casti roviny 4
↑ johny0222:
42. Obrazec je symetrický podle osy y, stačí tedy vyřešit pravou část a výsledek se nakonec vynásobí dvojkou.
Obsah vymezený oběma osami a parabolou 8-x^2 je:
Nyní musíme odečíst plochu pod parabolou x^2. Tuto plochu rozdělíme na dvě, první je od nuly do 2, druhá od 2 do 2√2.

A nyní zbývá obě plochy pod parabolou x^2 odečíst od plochy pod parabolou 8-x^2. .
.
A poslední krok - máme jen půlku požadované plochy, tedy výsledek vynásobíme dvojkou a dostaneme 
P.S. Ostatní příklady obdobným způsobem. Výpočet integrálů jsem neuváděl, přijde mi jednoduchý. V případě nejasností ještě napište.
Offline
#8 10. 06. 2010 07:30
Re: Plosny obsah casti roviny 4
pri tej 42 by sa to nemohlo robit aj tak ze by bolo (8-x^2-x^2) a medze by boli 0 a 2 a -2 a 0 a pocitalo by sa to cez 2 integrali , ktore by sa na konci scitali .... vysledom mal ale vyjst 64/3
43 - ako upravit ten vyraz x^4/16 +x^4/4-2 ... a tiez by sa to potom pocitalo cez korenove body, 2 integralz a rovnakz postup
44 -ako teda dalej, kedye tam mam to x^3-1 ?
Offline
#9 10. 06. 2010 10:46
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Plosny obsah casti roviny 4
↑ johny0222:
Zde platí také stejné doporučení.
42) dálo by se počítat, že integruješ rozdíl ("horní funkce" - "dolní funkce"), jak navrhuješ. Stačí integrovat na interval 0 až 2 a výsledek vynásobit dvojkou. Obrázek je symetrický.
43) celou rovnici vynásobit 16. Hledáš kořeny této rovnice. Nalezené x_1, x_2 budou meze po x pro integral. Také lze počítat za polovinu plochy.
44) x(x^3-1)=0, pro rozklad závorky - viz užitečný vzorec.
Offline
#10 10. 06. 2010 12:19
Re: Plosny obsah casti roviny 4
42, 44 ..ok
potrebujem este poradit s tou 43
dal som tam 2 sposoby ako by sa asi mohlo pokracovat
- v prvom mi vznikli moc velke cisla, co mylsim ze by asi nebolo dobre s nimi dalej pocitat
- v druhom pripade zas x^2+4 co nebude nikdy nula
Offline
#11 10. 06. 2010 16:44 — Editoval jelena (10. 06. 2010 21:09)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Plosny obsah casti roviny 4
↑ johny0222:
Zajimavé způsoby, ale ani jedním nebudeme pokračovat.
řešíme rovnici  , pokud to nejde v tomto tvaru, tak substituce
, pokud to nejde v tomto tvaru, tak substituce 
 , řešením jsou
, řešením jsou  ,
,  , zpět do substituce použijeme pouze hodnotu 4, jelikož 2. mocnina nemůže být číslo záporné.
, zpět do substituce použijeme pouze hodnotu 4, jelikož 2. mocnina nemůže být číslo záporné.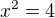 , odsud
, odsud  ,
, 
Řekla bych, že celý problém je v řešení rovnic v součinovém tvaru, s integrálem problém nemáš.
-------
"... сказала...."
Offline
#15 12. 06. 2010 09:32
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Plosny obsah casti roviny 4
↑ johny0222:
výraz pod odmocninou nemůžeš rozdělit tak, jak jsi provedl. Ve výsledku po integrování má být - viz vzorec 30.
nemůžeš rozdělit tak, jak jsi provedl. Ve výsledku po integrování má být - viz vzorec 30.
Zkontroluj svůj postup integrování "tohoto kousku" tady - v MAW.
Offline
#17 12. 06. 2010 14:41
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Plosny obsah casti roviny 4
↑ johny0222:
tg^(-1) je jiný zápis pro arctg. Bude třeba v tomto smyslu opravit.
Offline
#19 12. 06. 2010 22:24 — Editoval jelena (12. 06. 2010 22:26)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Plosny obsah casti roviny 4
↑ johny0222:
odkazovaný vzorec je pro  , proto zápis je treba upravit takto
, proto zápis je treba upravit takto  , vzorec platí pro orámovanou část. Toho už jsem si mohla všimnout při předchozí kontrole, omluva.
, vzorec platí pro orámovanou část. Toho už jsem si mohla všimnout při předchozí kontrole, omluva.
Pokud ve výsledku bude arctg(...čeho...), tak se to ještě zapíše jako tabulková hodnota nebo výpočtem na kalkulaččce. Třeba arctg(1)=pi/4
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Plosny obsah casti roviny 4 (TOTO TÉMA JE VYŘEŠENÉ)






