Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 14. 06. 2010 20:57
- ondrej.hav
- Příspěvky: 162
- Reputace: 4
Řada
Pěkný večer. Chtěl bych se zeptat, když mám řadu 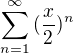 A chci zjistit obor konvergence. Tak si vypočítám nutnou podmínku konvergence tj.
A chci zjistit obor konvergence. Tak si vypočítám nutnou podmínku konvergence tj. 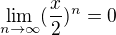 zjistím že to platí pro
zjistím že to platí pro  A pak použiju ještě nějaké kritérium? Tak jsem zkusil třeba limitní odmocninové
A pak použiju ještě nějaké kritérium? Tak jsem zkusil třeba limitní odmocninové ![kopírovat do textarea $K= \lim_{n\rightarrow \infty}\sqrt[n]{(\frac{x}{2})^n}$](/mathtex/11/11133b59ebaee6cfe5c2011d458162e1.gif) tudíž
tudíž  a protože řada konverguje pro K < 1 tak položím
a protože řada konverguje pro K < 1 tak položím  a dostanu
a dostanu  A co teď? Teď to mam porovnat s tou nutnou podmínkou? Já sem viděl i že se tam dala absolutní hodnota, ale tim bych přeci určil interval abolutní konvergence a ne obyčejné? Nebo ty intervaly jsou stejné?a rozhoduju jenom o tom jestli sou abolutní nebo neabsolutní? Moc tomuto problému celkově nerozumím. Je to na mě až moc abstarktní
A co teď? Teď to mam porovnat s tou nutnou podmínkou? Já sem viděl i že se tam dala absolutní hodnota, ale tim bych přeci určil interval abolutní konvergence a ne obyčejné? Nebo ty intervaly jsou stejné?a rozhoduju jenom o tom jestli sou abolutní nebo neabsolutní? Moc tomuto problému celkově nerozumím. Je to na mě až moc abstarktní
Offline
- (téma jako vyřešené označil(a) ondrej.hav)
#3 14. 06. 2010 21:09
Re: Řada
Z absolutní konvergence plyne běžná konvergence. Výpočtem ![kopírovat do textarea $\lim_{n \to \infty} \sqrt[n]{\|\frac x2\|^n}$](/mathtex/81/81a0de1b6def499ff8efaabc5e9d7547.gif) zjistíš, kde řada absolutně konverguje, a podle nutné podmínky konvergence pak zjistíš, že "všude jinde" diverguje.
zjistíš, kde řada absolutně konverguje, a podle nutné podmínky konvergence pak zjistíš, že "všude jinde" diverguje.
Offline
#4 14. 06. 2010 21:11
- ondrej.hav
- Příspěvky: 162
- Reputace: 4
Re: Řada
↑ jarrro:Jo, jasny, takze kdyz mam radu ktera je geometricka, tak musim vyuzit toho vztahu pro geometrickou radu? Nejakyma tema kriteriama mi to nevyjde?
Offline
#5 14. 06. 2010 21:14
- ondrej.hav
- Příspěvky: 162
- Reputace: 4
Re: Řada
↑ Olin:Jo takhle už mi to taky vychází... :-) Ale jak přijdu na tu absolutní hodnotu? Já bych to totiž napsal takto: ![kopírovat do textarea $\lim_{n \to \infty} \sqrt[n]{\|\frac{x}{2}^n\|}$](/mathtex/a3/a397b1f3ba1b0d72402442b2d925c033.gif) A s tím už si nevím rady... Nebo to můžu upravit z toho mého na to tvoje?
A s tím už si nevím rady... Nebo to můžu upravit z toho mého na to tvoje?
Offline
#6 14. 06. 2010 21:17 — Editoval jarrro (14. 06. 2010 21:20)
Re: Řada
↑ ondrej.hav:↑ ondrej.hav:vyjde,ale geometrické rady sú veľmi jednoduché a použitie kritérií je kanón na vrabce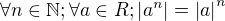
MATH IS THE BEST!!!
Offline
#7 14. 06. 2010 21:18 — Editoval ondrej.hav (14. 06. 2010 21:21)
- ondrej.hav
- Příspěvky: 162
- Reputace: 4
Re: Řada
↑ jarrro:Když já mám pak i těžší a tam už musím používat kritéria... :-( A díky mooc
Offline
#8 14. 06. 2010 21:51
- ondrej.hav
- Příspěvky: 162
- Reputace: 4
Re: Řada
↑ jarrro:Prosím ještě bych se chtěl zeptat jak tu řadu sečtu?
Offline
#10 14. 06. 2010 22:04
- ondrej.hav
- Příspěvky: 162
- Reputace: 4
Re: Řada
mělo by to být 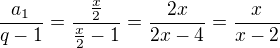 ale podle výsledků na vebu matematické analýzy je
ale podle výsledků na vebu matematické analýzy je 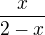 Tak já nevím :-(
Tak já nevím :-(
Offline
#11 14. 06. 2010 22:06
Offline
#12 14. 06. 2010 22:07
- ondrej.hav
- Příspěvky: 162
- Reputace: 4
Re: Řada
↑ jarrro:AAAAAAAha... neumim ani opisovat... :-(
Offline


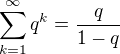 teda (prvý člen)/(1-kvocient) čo sa ľahko dokáže lebo
teda (prvý člen)/(1-kvocient) čo sa ľahko dokáže lebo 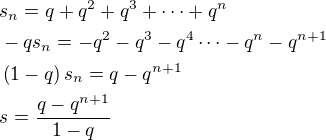 keď n pošleme do nekonečna tak pre
keď n pošleme do nekonečna tak pre  je
je