Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 15. 06. 2010 17:55
- ondrej.hav
- Příspěvky: 162
- Reputace: 4
Mocninná řada
Pěkné odpoledne, ty řady mě jednou zničí... Mám tady mocninnou řadu a potřebuju si ověřit svoje úvahy. Mám například řadu 
Určím střed tj 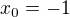
Pak si určím poloměr jako ![kopírovat do textarea $\lim_{n\rightarrow \infty}{\sqrt[n]{\left|\frac{1}{2^n n}\right|}}$](/mathtex/3b/3b15bb59bbfc5c7a57fb0b0183b08e12.gif) a vyjde mi 2. Tudíž interval konvergence
a vyjde mi 2. Tudíž interval konvergence 
Předpokládám, že tohle určení je jakási výhoda u mocninných řad. Ale stejně bych to spočetl třeba přes Cauchyho kritérium. Doufám... hlavně je nějak podezřele podobný :-) A když chci určit
Obor konvergence tak ten bude vždy shodný s  . Ažna krajní body. Předpokládám, že
. Ažna krajní body. Předpokládám, že  je vždy otevřený interval a
je vždy otevřený interval a  může být nejvýše rozšíření
může být nejvýše rozšíření  o krajní body?
o krajní body?
Tudíž zkusím dosadit 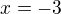 dostanu
dostanu  a ta podle Leibnitzova kritéria KONVERGUJE
a ta podle Leibnitzova kritéria KONVERGUJE
pak zkusím dosadit  a dostanu
a dostanu  tato řada (snad to nemusím ověrovat??) DIVERGUJE
tato řada (snad to nemusím ověrovat??) DIVERGUJE
Takže 
A ted si nejsem jistej jak je to s ABSOLUTNÍ konvergencí. Jelikož jsem na začátku použil to s tou odmocninou a absolutní hodnotou, řekl bych, že sem tím jakoby ověřil absolutní konvergenci... Tudíž bude (automaticky?????) 
Offline
- (téma jako vyřešené označil(a) ondrej.hav)
#2 15. 06. 2010 18:35
Re: Mocninná řada
Každá mocninná řada (tedy řada tvaru  ) má určitý "kruh konvergence" - tj. interval
) má určitý "kruh konvergence" - tj. interval  , kde
, kde  je střed řady a
je střed řady a  poloměr konvergence - na kterém konverguje absolutně. Je to vždy buď otevřený interval, nebo celé
poloměr konvergence - na kterém konverguje absolutně. Je to vždy buď otevřený interval, nebo celé  , nebo pouze jednoprvková množina
, nebo pouze jednoprvková množina  . Pro
. Pro  a
a  pak řada diverguje. Toto se dokazuje velmi jednoduše pomocí Cauchyho odmocninového kritéria, proto ta podobnost ve výpočtu.
pak řada diverguje. Toto se dokazuje velmi jednoduše pomocí Cauchyho odmocninového kritéria, proto ta podobnost ve výpočtu.
O konvergenci v bodech  a
a  obecně nevíme nic, a tak se vyšetřují zvlášť. V podstatě jsou tyto čtyři možnosti:
obecně nevíme nic, a tak se vyšetřují zvlášť. V podstatě jsou tyto čtyři možnosti:
1) v obou bodech řada konverguje absolutně
2) v obou konverguje neabsolutně
3) v jednom z bodů řada konverguje neabsolutně, v druhém diverguje
4) v obou diverguje.
Ve výše uvedené řadě máme podle této teorie už zaručeno, že na intervalu  konverguje absolutně. V jedničce řada diverguje, v -3 konverguje, ale pouze neabsolutně, protože
konverguje absolutně. V jedničce řada diverguje, v -3 konverguje, ale pouze neabsolutně, protože  , což nám dá divergentní řadu.
, což nám dá divergentní řadu.
Offline
#4 15. 06. 2010 20:20
- ondrej.hav
- Příspěvky: 162
- Reputace: 4
Re: Mocninná řada
↑ ondrej.hav:Jen se ještě zeptám, to že můžpou nastat jenom ty 4 možnosti se dá nějak dokázat? Nebo odvodit (logicky) ??? Proč se nemůže stát, že by v jednom bodě konvergovala absolutne a v druhem neabsolutne???
Offline
#5 15. 06. 2010 20:28
Re: Mocninná řada
Dá se to dokázat poměrně snadno. Pro  totiž máme řadu
totiž máme řadu
a pro  to je
to je .
.
Jestliže absolutně konverguje jedna z řad, pak absolutně konverguje i ta druhá, jelikož  .
.
Offline