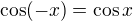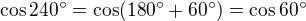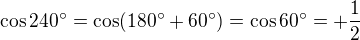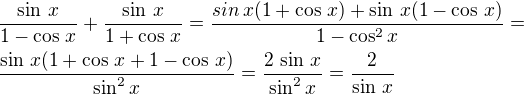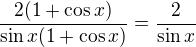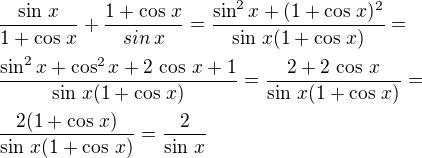Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 15. 06. 2010 20:44
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Goniometrické funkce
Ahoj, pomůžete mi prosím najít chybu? Má to vyjít -1 a nemůžu najít chybu. Děkuju
Offline
- (téma jako vyřešené označil(a) Lucinecka88)
#3 15. 06. 2010 20:58
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: Goniometrické funkce
Právě že ne, má tam být mínus.
Offline
#6 15. 06. 2010 21:01
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: Goniometrické funkce
všechno má být tak jak jsem to napsala
Offline
#7 15. 06. 2010 21:16
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: Goniometrické funkce
Nechápu co mi tady píšeš. Kde mám prosím tu chybu?
Offline
#8 15. 06. 2010 21:19
Re: Goniometrické funkce
jen jsem zkoušela hledat chybu ... buď se první dva členy sčítají nebo poslední dva násobí nebo prostě nevím .... zkus počkat na další rady
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#12 15. 06. 2010 21:48
Offline
#13 15. 06. 2010 23:54
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Goniometrické funkce
↑ gadgetka: asi jen překlep, je to tak? Děkuji.
Offline
#15 16. 06. 2010 00:30
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Goniometrické funkce
myslím, že toto není OK:
.
V zadání (nebo ve výsledku) je možný překlep (pokud Lucinečka chape postup, tak u maturity to zvladne), ale převádět radiany na stupně je zhůvěřilost (c). :-)
Offline
#16 16. 06. 2010 07:35
Re: Goniometrické funkce
Aha ... třetí kvadrant, fce cos záporná, násobek 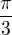 , tak proto
, tak proto 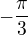 , ano? Je vidět, že už jsem toho hodně zapomněla ... omlouvám se a jdu se stydět :)
, ano? Je vidět, že už jsem toho hodně zapomněla ... omlouvám se a jdu se stydět :)
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#17 16. 06. 2010 09:58
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: Goniometrické funkce
Děkuji, ještě bych poprosila o pomoc s příkladem. Nevím jak mám pokračovat.
Offline
#18 16. 06. 2010 10:15 — Editoval Cheop (16. 06. 2010 10:18)
#19 16. 06. 2010 10:22
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: Goniometrické funkce
↑ Cheop:
Děkuji. To mě vůbec nenapadlo.
Offline
#20 16. 06. 2010 10:31
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: Goniometrické funkce
Děkuji. Ještě prosím o radu jak mám pokračovat. 
Offline
#21 16. 06. 2010 10:41
Offline