Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 16. 06. 2010 15:16
Hyperbola
Ahojky, prosim vas o pomoc, nemuzu na to vubec prijit :(
Je zadaná funkce f(x) = = 8 − 4x / −2x + 3.
Mám najít průsečíky, Df a Hf a střed hyperboly. Priblizne to chapu, ale bohuzel to neumim upravit aby mi to vyslo :(
Děkuji za pomoc
Offline
- (téma jako vyřešené označil(a) jelena)
#2 16. 06. 2010 15:34 — Editoval gadgetka (16. 06. 2010 15:46)
Re: Hyperbola
Průsečíky: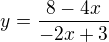
Dosaď y=0 a získáš průsečík s x-ovou souřadnicí a pak x=0 a dostaneš průsečík s y-ovou souřadnicí.
H(f):
pro fci 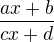 , kde
, kde 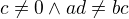 platí:
platí: 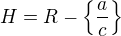 a
a 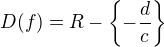
Středem hyperboly procházejí asymptoty:
asymptota || s osou x: 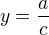
asymptota || s osou y: 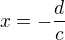
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#4 16. 06. 2010 16:01
Re: Hyperbola
Offline
#5 16. 06. 2010 16:11
Offline
#7 16. 06. 2010 17:45 — Editoval gadgetka (16. 06. 2010 17:50)
Re: Hyperbola
a ještě dotaz, před osmičkou je mínus nebo jsi jen napsal dvakrát rovná se?
Podle průsečíků mi to došlo ... jen dvakrát rovná se :)
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline