Matematické Fórum

Dr.Silenec

Zdravim,

mám problém mám sestrojit trojúhelník, když znám stranu a, ta, tb... můžete mě prosím někdo navést jak na to?

a druhý příklad se týká trošku složitějšího příkladu se, kterým si vůbec nevím rady.. Zadání:

V příkladech jsou a,b,c,d,m,n dané úsečky. Sestrojte úsečku x, pro kterou platí: 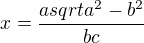$x=\frac{a sqrt{a^2-b^2}}{bc}$

Díky moc za pomoc

BakyX · 17. 06. 2010 14:22 — Editoval BakyX (17. 06. 2010 14:24)

Načrtni si trojuholník a tie ťažice doň. Teraz si ho doplň na rovnobežník tak, aby jedna jeho strana bola úsečka BC (strana "a"). Stred strany AC je vlastne bod, z ktorého je vedená ťažnica. Je to aj priesečník uhlopriečok rovnobežníka. Preto predĺžená ťažnica sa dotýka bodu rovnobežníka. Ak máš načrtnuté obe ťažnice, vidíš ťažisko. Vzdialenosť bodu A od ťažiska poznáš. Stranu rovnobežníka tiež. Vzdialenosť ťažiska od bodu, ktorym sme doplnili rovnozenik tiez. Preto to môžeš narysovať. Zvyšok nie je problém. (keby si nerozumel, skusim hodiť náčrt)

V tom druhom - môžeš prepísať od slova do slova zadanie ? Niejako tomu nerozumiem

jelena · 17. 06. 2010 23:16

↑ BakyX:

Zdravím, zřejmě se jedná o konstrukci algebraických výrazů (nebo algebraická metoda řešení konstrikcí) - materiál, str. 30 cca.

↑ Dr.Silenec: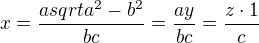

$x=\frac{a sqrt{a^2-b^2}}{bc}=\frac{ay}{bc}=\frac{z\cdot 1}{c}$

postupně sestrojím: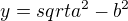

$y=sqrt{a^2-b^2}$ pomocí Pythagorovy věty sestrojím délku úsečky = odvěsná pravoúhlého trojuhelníku s přeponou a, druhou odvesnou b.

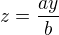$z=\frac{ay}{b}$ pomocí čtvrté geometrické úměrné.

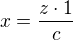$x=\frac{z\cdot 1}{c}$ - pomocí čtvreté geometrické úměrné s použitím jedné úsečky o jednotkové délce.

Může být? Děkuji.

Matematické Fórum

#1 17. 06. 2010 14:03 — Editoval Dr.Silenec (17. 06. 2010 14:03)

Trojúhelníky - Planimetrie příklady

#2 17. 06. 2010 14:22 — Editoval BakyX (17. 06. 2010 14:24)

Re: Trojúhelníky - Planimetrie příklady

#3 17. 06. 2010 23:16

Re: Trojúhelníky - Planimetrie příklady

Zápatí