Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 17. 06. 2010 00:52 — Editoval ondrej.hav (17. 06. 2010 16:01)
- ondrej.hav
- Příspěvky: 162
- Reputace: 4
Shodnost křivek
Pěkný večer, potřeboval bych pomoct s příkladem typu najdi interval I takový, že křivka je na něm shodná........
Konkrétní příklad: 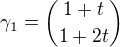 a
a 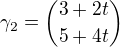 u té první
u té první 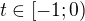 a mám zvolit
a mám zvolit  tak aby
tak aby 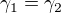
Mě osobně napadl způsob že bych vzal krajní bod toho intervalu, který znám tj. -1 a dosadil bych ho do příslušné křivky...
Tj. 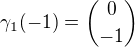 a spočtu z té druhé křivky pro jaké t je
a spočtu z té druhé křivky pro jaké t je 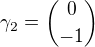
No a pak udélám to samé pro ten druhý kkrajní bod... To ale prý není uplně dobrý řešení... Tak jestli by mi nekdo poradil nejaky jiny zpusob?
Hlavně kdž mam třeba křivky s goniometrickymi funkcemi tak to reseni nebyva uplne jednoznečné...
PROSÍM PROSÍM, MŮŽETE MI NĚKDO PORADIT???
Offline
- (téma jako vyřešené označil(a) ondrej.hav)
#3 17. 06. 2010 16:04 — Editoval Rumburak (17. 06. 2010 16:05)
Re: Shodnost křivek
Obecně lze ihned říci, že každá z křivek je částí (nějaké) přímky a jde-li o dvě přímky, mají stejný směr (protože jejich směrové vektory
jsou lin. závislé).
Definiční obor první křivky rozšíříme i na hodnotu t = 0 , v tomto bodě pak bude 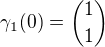
Máme tedy 2 body prvé křivky a najdeme-li je i na druhé křívce, znamená to, že tyto body omezují úsečku společnou oběma křivkám.
Krajním bodům této křivky v druhém popisu odpovídají krajní body intervalu pro parametr a ten krajní bod, který opovídá bodu 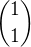 ,
,
vyloučíme, abychom získali křivku odpovídající křivce 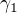 v její původní versi.
v její původní versi.
Offline
#4 17. 06. 2010 17:22
- ondrej.hav
- Příspěvky: 162
- Reputace: 4
Re: Shodnost křivek
↑ Rumburak: Dekuji, a ještě se zeptám, tenhle postup můžu použít pro jakékoli křivky? Přotože právě tohle se mi docela osvědčilo... Ale náš cvičící tam používá nějaký porovnávání a vždyky z toho vyseparuje ještě předpis... nějakej jakože ne parametrickej, nevim jak se jmenuje... No a to mi přijde dost složitý. a pak tam nějak ten interval z toho takovym zajimavym zpusobem dostane... "nějak" Tuto se mi fakt líbí víc... Akorát se chci zeptat jestli je to obecně aplikovatelný na jakýkoli příklad....
Offline
#5 17. 06. 2010 18:35
- kaja(z_hajovny)

- Místo: Lážov
- Příspěvky: 1002
- Reputace: 12
- Web
Re: Shodnost křivek
↑ ondrej.hav:
jestli tomu dobre rozumim, porovnavate jenom krajni body a pokud jsou stejne, rad byste tvrdil, ze krivkz jsou cele stejne. takze si asi uz dokazete odpovedet sam.
Offline
#6 17. 06. 2010 22:39
- ondrej.hav
- Příspěvky: 162
- Reputace: 4
Re: Shodnost křivek
↑ kaja(z_hajovny):Hmmm já vím, že na nějkakém intervalu ty křivky stejné jsou. Hledám jenom ten interval kde to platí... v tom případě bych to tak mohl udělat ne? Nebo jestli ne, tak jestli byste mi mohl, prosím, poradit nějakou jinou metodu?
Offline
#7 17. 06. 2010 23:01
- kaja(z_hajovny)

- Místo: Lážov
- Příspěvky: 1002
- Reputace: 12
- Web
Re: Shodnost křivek
Dosavadni diskuze byla bud dost vagni nebo se jednalo o cast primky. Bylo by mozne se dat Vas postup pro nejaky mene trivialni priklad, at muzeme posoudit, jestli to delate dobre nebo spatne?
Ja bych se asi snazil najit neparametrickou rovnici
Offline
#8 17. 06. 2010 23:24 — Editoval ondrej.hav (17. 06. 2010 23:34)
- ondrej.hav
- Příspěvky: 162
- Reputace: 4
Re: Shodnost křivek
↑ kaja(z_hajovny):Tak dejme tomu 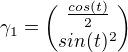 a
a  a
a 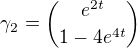
EDIT: Což mojí metodou vychází podle výsledků správně.....
Počítám jako 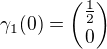 tudíž musí platit rovnice
tudíž musí platit rovnice 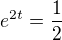 což platí pro
což platí pro 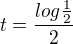 Stejně tak musí vyjít rovnice
Stejně tak musí vyjít rovnice 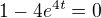 Což vyjde....
Což vyjde....
pak vezmu 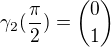 tudíž musí vyhovovat rovnici
tudíž musí vyhovovat rovnici 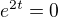 což platí pro
což platí pro 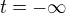
A dostávám interval 
Offline
#9 18. 06. 2010 09:14
- kaja(z_hajovny)

- Místo: Lážov
- Příspěvky: 1002
- Reputace: 12
- Web
Re: Shodnost křivek
pokud v prvni krivce zmenime sin^2(x) za sin^3(x) tak evidentne vse zustane v platnosti a proto by tahle nova krivka taky mela byt stejna jako krivka gamma_2. Coz je nesmysl (skuste si namalovat).
Pro Sage treba nejak takto:
Code:
t=var('t')
P1=parametric_plot((cos(t)/2,(sin(t))^2),(t,0,pi/2))
P2=parametric_plot((exp(2*t),1-4*exp(4*t)),(t,-10,log(1/2)/2),color='red')
P3=parametric_plot((cos(t)/2,sin(t)^3),(t,0,pi/2),color='green')
P3+P1+P2Prvni dve krivkyjsou stejne, protoze to je zakamuflovana parabola y=1-4*x^2, treti krivka je jina, podle Vaseho vypoctu by ale mela byt stejna.
Offline
#10 18. 06. 2010 09:45 — Editoval Rumburak (18. 06. 2010 09:58)
Re: Shodnost křivek
↑ ondrej.hav:
Danou křivku tvoří nějaký funkční či relační vztah - obecně třeba F(x,y) = 0 - platný pro každý bod [x,y] té křivky (F je funkce charakteristická
pro tu křivku) a tento vztah musí být zachován i při přechodu k parametrickému vyjádření té křivky, tj. musí být pak splněno F(x(t),y(t)) = 0 .
Pokud by parametrické vyjádřeni x = x(t) , y = y(t) na určitém intervalu nesplňovalo vztah F(x(t),y(t)) = 0 , pak by příslušná křivka nebyla
částí křivky o rovnici F(x,y) = 0 (na krajní body ani orientaci křivek teď nehleďíme) .
Odtud plyne, jak rozhodnout, zda dvěma parametrickými vyjádřeními je popsána tatáž křivka .
Křivka 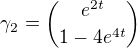 splňuje rovnici
splňuje rovnici  a tutéž rovnici splňuje i křivka
a tutéž rovnici splňuje i křivka 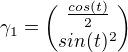 ,
,
takže při vhodné volbě počátečních a koncových bodů mají křivky tytéž trajektorie neboli geometrické obrazy, neboli: jsou totožné, pokud
nehledíme na orientaci. Zda se křivky shodují i co do orientace, to nutno posoudit další úvahou, která je, myslím, zřejmá.
Pozn. Vyšel jsem z předpokladu, že zápisem 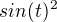 je míněno
je míněno 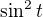 .
.
Offline
#11 18. 06. 2010 14:25
- ondrej.hav
- Příspěvky: 162
- Reputace: 4
Re: Shodnost křivek
↑ Rumburak:To znamená, že před řešením bych měl ještě udělat jeded krok a to "odparametrizování" těch dvou křivek... ??? Pokud my vyjde stejnáá závislos y na x u obou křivek moho s klidem použít ten můj postup??? Je to tak?
Offline
#12 18. 06. 2010 14:37 — Editoval Rumburak (18. 06. 2010 14:49)
Re: Shodnost křivek
↑ ondrej.hav:
Ano, ten krok "odparametrizace" je důležitý, to bude nejpíš ten postup vašeho cvičícího, kterému jsi nepříliš rozuměl.
EDIT. Ale ani zde není radno postupovat bez rozmyslu. Problém může nastat u křívek, jejichž obecná rovnice je
v implicitním tvaru F(x,y) = 0, jako třeba u kružnice o rovnici x^2 + y^2 = 1 , jejíž body [-1,0], [1,0] jsou společné
dvěma různým obloukům (jeden nad osou x a duhý pod osou x).
Pokud ale je svrchu jasné, že jde o dvě par. rovnice přímky (tak jako v té první úloze), pak tento krok dělat nemusíme,
protože o dvou přímách platí, že mají-li společné dva různé body, jsou totožné. Jiné křivky než přímky však takovou
vlastnost nemají.
Offline
#13 18. 06. 2010 16:30
- ondrej.hav
- Příspěvky: 162
- Reputace: 4
Re: Shodnost křivek
↑ Rumburak:Jo díky mooc... to opravdu bude ono...
Offline