Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 19. 06. 2010 16:03 — Editoval Siroga (19. 06. 2010 16:09)
moivreova veta
potreboval bych mensi radu, mam priklad : 
mam to resit moavrovou vetou, vychazi mi ze 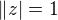
a ze 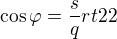
a 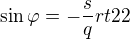
a nevim jak se dal urci kolik je to 
jako kolik  se rovna
se rovna 
Jstlž jst schpn přčst tt, mžt njt dbr zmstnn jk prgrmtr.
Offline
- (téma jako vyřešené označil(a) jelena)
#2 19. 06. 2010 16:06
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: moivreova veta
To není příklad, to je výraz.
Chceš ho upravit? Třeba do algebraického tvaru? Nebo snad něco jiného?
Edit: Pokud je z rovno tomu výrazu, pak skutečně 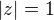 .
.
Offline
#4 19. 06. 2010 16:13
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: moivreova veta
↑ Siroga:
Abychom mohli řešit, tak musíme znát zadání. To jsi stále celé nenapsal. Podle zadání se pak volí kroky, které povedou k jeho vyřešení.
Pokud  je argument komplexního čísla v závorce, pak souhlasím, že
je argument komplexního čísla v závorce, pak souhlasím, že 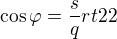 a
a 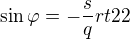 .
.
Jestliže chceš určit  , pak ho hledej jako řešení soustavy dvou rovnic. Pro která
, pak ho hledej jako řešení soustavy dvou rovnic. Pro která  platí
platí 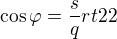 a zároveň
a zároveň 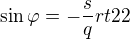 ?
?
Offline
#5 19. 06. 2010 16:15
Re: moivreova veta
koukal sem tady : http://www.matweb.cz/komplexni-cisla na ten prevod na goniometricky tvar a nechapu kde se prijde na to kolik je to 
oni tam maji "Převeďte komplexní číslo 6 − 6i. Jako první si nyní spočítáme |z|, absolutní hodnotu čísla. Ta se rovná √72, což můžeme upravit na 6√2 (nejprve číslo převedeme na √(36·2) a poté odmocníme šestku a dvojku ponecháme). Nyní musíme spočítat hodnotu φ. Víme, že cos φ = a/|z|, po dosazení dostáváme cos φ = 6/6√2 = 1/√2 = √2/2. Z tohoto nám vychází, že φ se rovná buď π/4 anebo 7π/4.
Teď se vrhneme na druhou část. Víme, že sin φ = b/|z|, po dosazení dostáváme sin φ = −6/6√2, po úpravách vychází sin φ = −√2/2. Hodnota φ může nabývat hodnot 5π/4 nebo 7π/4. Vidíme, že sinus i kosinus mají stejný výsledek při hodnotě φ = 7π/4."
a mne nejak neleze do hlavy kde se bere to "φ se rovná buď π/4 anebo 7π/4" a "Hodnota φ může nabývat hodnot 5π/4 nebo 7π/4"
Jstlž jst schpn přčst tt, mžt njt dbr zmstnn jk prgrmtr.
Offline
#7 19. 06. 2010 16:18
Re: moivreova veta
http://2i.cz/6dd9f2d80b <- takhle vypada maturitni otazka, a ucitelka rekla ze se to maresit pomoci moavrovy vety tak ja nevim co v tom zadani jeste chybi :D
Jstlž jst schpn přčst tt, mžt njt dbr zmstnn jk prgrmtr.
Offline
#9 19. 06. 2010 16:20
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: moivreova veta
Pokud znáš funkci  , pak víš, že v nule nabývá hodnoty nula, pak roste, maxima (jedničky) nabývá v bodě
, pak víš, že v nule nabývá hodnoty nula, pak roste, maxima (jedničky) nabývá v bodě 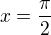 , pak klesá, v
, pak klesá, v  nabývá opět nulové hodnoty atd. Pak bys měl také znát významné hodnoty funkce sinus (např. že
nabývá opět nulové hodnoty atd. Pak bys měl také znát významné hodnoty funkce sinus (např. že  apod.). Těchto znalostí využiješ k tomu, abys našel všechna řešení rovnice
apod.). Těchto znalostí využiješ k tomu, abys našel všechna řešení rovnice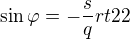
na intervalu  . To je jasné?
. To je jasné?
Offline
#11 19. 06. 2010 16:22
Offline
#13 19. 06. 2010 16:27
Re: moivreova veta
↑ b.r.o.z1: jak se na to prijde? tohle sme se ucili uz snad na zakladce a ja to nejak porad nechapu :D
Jstlž jst schpn přčst tt, mžt njt dbr zmstnn jk prgrmtr.
Offline
#15 19. 06. 2010 16:28
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: moivreova veta
↑ Siroga:
To "vypočítejte" ti tam chybělo :-). Může to vypadat nadbytečně, ale mohl bych ti vymyslet spoustu jiných zadání se stejným výrazem a každé by se lišilo v řešení.
Offline
#17 19. 06. 2010 16:29 — Editoval Siroga (19. 06. 2010 16:30)
Re: moivreova veta
no zatim chapu ze kdyz teda cos mam kladne tak je v 1 nebo 4 kvadrantu , a sin zaporne tak v 3 nebo 4 kvadrantu => fi bude v 4 kvadrantu
↑ b.r.o.z1:
no skoro znam , akorat nevim jak se z cos fi a sin fi dostane kolik je fi pi
Jstlž jst schpn přčst tt, mžt njt dbr zmstnn jk prgrmtr.
Offline
#18 19. 06. 2010 16:33 — Editoval Siroga (19. 06. 2010 16:34)
Re: moivreova veta
↑ b.r.o.z1:
na goniometricky tvar sem to prave prevadel v prispevku 1 a zjistil sem jen 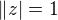 ,
,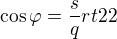 ,
,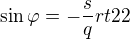 a v tuhle chvili ma prijit na radu vykouzleni ze
a v tuhle chvili ma prijit na radu vykouzleni ze 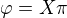 a ja nevim jak to vykouzlit :d
a ja nevim jak to vykouzlit :d
Jstlž jst schpn přčst tt, mžt njt dbr zmstnn jk prgrmtr.
Offline
#19 19. 06. 2010 16:34 — Editoval b.r.o.z1 (19. 06. 2010 16:40)
Re: moivreova veta
↑ Siroga:
ok tak od píky ;-)
|z|=1 - normální výpočet velikosti komplexního čísla, umocníš na druhou reálnou část sečteš s umocněnou imaginární částí => odmocníš a máš velikost |z|
z1 = reálná část = 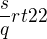
z2 = imaginární část = 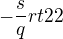
http://cs.wikipedia.org/wiki/Komplexn%C … D.C3.ADsel
Goniometrický tvar komplexního čísla
cos fí = (z1)/(|z|)
sinfí = (z2)/(|z|)
=> cos fí = 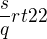
sin fí = 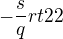
cos je kladný v I. a IV. kvadrantu
sin je záporný v III. a IV.kvadrantu
=> víme že úhel je ve IV. kvadrantu a odpovídá hodnotě pro sin = 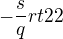 a pro cos=
a pro cos= 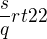
pak kouknu buď do hlavy nebo na tabulku hodnot a hodnota 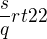 je pí/4, ale já jsem ve IV. kvadrantu takže 2pí - pí/4 = 7/4 pí = NÁŠ ÚHEL
je pí/4, ale já jsem ve IV. kvadrantu takže 2pí - pí/4 = 7/4 pí = NÁŠ ÚHEL
teď už se to jen zapíše v goniometrickém tvaru: z=1(cos7/4pí + i sin7/4pí)
"Vím, že nic nevím." Sokrates
Offline
#20 19. 06. 2010 16:37
Re: moivreova veta
↑ b.r.o.z1:presne tohle umim a chapu :d a dal nevim :d
Jstlž jst schpn přčst tt, mžt njt dbr zmstnn jk prgrmtr.
Offline
#23 19. 06. 2010 16:42 — Editoval b.r.o.z1 (19. 06. 2010 16:43)
Re: moivreova veta
↑ Siroga:
http://www.aristoteles.cz/matematika/fu … osinus.php
třeba tu nebo v Matematicko fyzikálních tabulkách
každopádně k maturitě z matematiky bys ji měl umět, hledání v tabulkách zbytečně zdržuje
"Vím, že nic nevím." Sokrates
Offline
 ?
?