Matematické Fórum

ondrej.hav · 20. 06. 2010 01:28

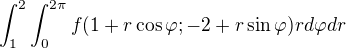Chtěl bych se zeptat ještě na jeden integrál: mám $\Omega={\{1\leq (x-1)^2+(y+2)^2}\leq 4\}$ a mě vyšlo $\int_{1}^{2}\int_{0}^{2\pi}f(1+r\cos{\varphi};-2+r\sin{\varphi})rd\varphi dr$ A v řešení je : 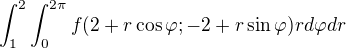$\int_{1}^{2}\int_{0}^{2\pi}f(2+r\cos{\varphi};-2+r\sin{\varphi})rd\varphi dr$ Jestliže tam ta dvojka je dobře a tudíž tam nedávám souřadnice středu, mohl by mi někdo prosím, poradit jak to spočítat?

kaja(z_hajovny)

tezko rict, nevim co bylo v zadani

bylo zadano 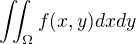$\iint_{\Omega}f(x,y)dxdy$ nebo neco jineho?

pokud to co pisu ja, tak spravne je varianta s jednickou.

ondrej.hav · 20. 06. 2010 12:33

↑ kaja(z_hajovny):Jo jo... zadání bylo nakkreslit tu oblast, a vypocist meze integralu, pak tu prevest na polarni souradnice, zakreslit a napsat meze integralu... :-D děkuji

Matematické Fórum

#1 20. 06. 2010 01:28

Integrál v polárních souřadnicích

#2 20. 06. 2010 07:14 — Editoval kaja(z_hajovny) (20. 06. 2010 07:15)

Re: Integrál v polárních souřadnicích

#3 20. 06. 2010 12:33

Re: Integrál v polárních souřadnicích

Zápatí