Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 23. 06. 2010 10:46
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Funkce
Ahoj, prosím o pomoc. U této funkce mám určit D(f), H(f), vrchol, graf funkce a průsečíky s osami. Jsem úplně ztracená. Děkuji
Offline
- (téma jako vyřešené označil(a) Lucinecka88)
#3 23. 06. 2010 10:58
Re: Funkce
řešení zde...
http://www.sdilej.eu/pics/4d4726dcdabaa … 1d3c8c.JPG
Ni moc, ni bohatství, jen vědění žezla trvají!
Offline
známe, 
známe. Nebojme se čísla, které půjde hůře odmocnit. Půjde alespoň částečně odmocnit.#7 23. 06. 2010 11:17 — Editoval LukasM (23. 06. 2010 11:19)
Re: Funkce
↑ Lucinecka88:
No vidíš, to je všechno dobře. Našla jsi i oba průsečíky s osami, dá se to ještě upravit na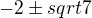 
. Teď si stačí uvědomit, že grafem funkce je parabola, a můžeš zhruba nakreslit graf.
Edit: haloganovi se omlouvám že jsem to na něm nenechal, když jsem se díval, byl jsi offline.
Offline
#8 23. 06. 2010 11:21
- frank_horrigan
- Příspěvky: 938
- Reputace: 31
Re: Funkce
Máš skoro všechno, ty průsečíky s osou x ti vyjdou jakoo kořeny té rovnice, kterou jsi rozpočítala, tedy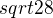 
si rozlož jako 
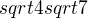, vytkni z celého čitatele dvojku a zkrať zlomek.
The only thing worse than being wrong is staying wrong
Sun Tzu - The Art of War
Offline
#10 23. 06. 2010 11:35
Re: Funkce
↑ Lucinecka88:
Všechny tři průsečíky jsou číselně vypočítány dobře, ale ten graf jim neodpovídá. Tvůj graf protíná osu y někde v záporných hodnotách, rozhodně ne ve trojce. Stejně tak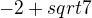 
je číslo o něco někde mezi nulou a jedničkou, ale tvůj graf protíná osu x odhadem tak v bodě [-0.2;0]. V mém minulém příspěvku je odkaz na graf vykeslený ve wolframu.
Offline