Matematické Fórum

Benny.RxT · 22. 06. 2010 17:15

Zdravim, nevysvětlil by mi někdo, jak se z kostry grafu určují hranové řezy?

Z definic vím, že hranový řez je taková jeho minimální množina hran, jejichž
odstraněním se stane graf nesouvislý.
Souvislý graf je zase takový neorientovaný graf v němž platí, že pro každé
dva vrcholy x,y existuje alespoň jedna cesta z x do y.

Ale pak například u tohoto grafu:

by podle knížky měli být tyto hran. řezy:

R1 = (1,6)
R2 = (2,5,6)
R3 = (3,5,6)
R4 = (4)

Ale nestačilo by podle definic jen:

R1 = (1) - k třem vrcholům nepovede cesta
R2 = (2, 3) - k dvoum vrcholům nepovede cesta

petrkovar

↑ Benny.RxT:
R1 = (1) nestačí, nevznikne nesouvilý graf.
R2 = (2, 3) by stačilo.
Taky by stačilo {1,2,5} a {1,3,5}.

Abych pravdu řekl, nevím proč při kostrukci řezu vycházet z kostry. Pokud jde o to najít nějaký řez, obvykle stačí vyhodit hrany incidentní s nějakým vrcholem.
Pokud jde o MINIMÁLNÍ řez (minimální vzhledem k ohodnocení) používají se toky.
Zkusím vymyslet alespoň nějaký algoritmus, třeba mi to někdo rozcupuje ;-)

1. Pak bych si našel kostru grafu a uvědomil si, že v každém řezu musí být alespoň jedna hrana vynechána (proč alespoň?).
2. Pak přidám některé ze zbývajících hran, co nejsou v kostře, aby graf zůstal nesouvislý.
Kolik takových možností je? To závisí na struktuře grafu a nenapadá mne pěkný (polynomiální) algoritmus na probrání všech možností.
Hrubou silou se dobereme k výsledku.

ondrej.hav

No, tak řezy se neurčují z kostry ale jaksi "ke kostře". Pokud chceš všechny, tak se to dá udělat pomocí fundamentální matice řezů. Ta ti potom bude generovat prostor všech řezů.

Postup... Zvolíš si v grafu kostru, pak (jakkoli) očísluješ hrany toho grafu. No vlastně ne jakkoli... Nejdřív musíš očíslovat všechny hrany kostry.... a pak zbyte... ale nijak nezáleží na pořadí.... No a pak si uděláš matici m*n kde m = počet hran kostry a n = počet hran....

důležité je, že tam matice bude obsahovat jednotkovou podmatici velikosti mxm...

no a potom budeš doplňovat jednotlivé řádky...

tak vezměš třeba ten první... tam je jednička na pozici 1,1... a teď napíšeš jedničky na minimální počet míst (reprezentující hrany které musím odebrat aby se zvýši počet komponent) nesmíš ale zasahovat do té podmatice... ta musí nutně zůstat JEDNOTKOVOU podmaticí...

Tak a ta matice se nazývá fundamentální matice řezů a generuje celý prostor řezů grafu...

Platí pro něj nějaká pravidla pro kolmost k libovolnému vektoru prostoru kružnic a tak dále... těch vlastností tam je hodně...

Pokud jsem to nenapsal dostatečně srozumitelně, tak dej vědět a já to zkusím rozepsat matematicky lépe a trošku pochopitelněji....

Za moment zkusím sem hodit řešení pro tvůj případ...

Jak jsem již psal ten prostor se bude vztahovat ke konkretní kostře... zvolil jsem kostru 1234... Definici kostry snad připomínat nemusím...
pro jistotu je to faktor který je stromem...

takže budeme mít matici 4x6
která bude obsahovat jednotkovou podmatici velikosti 4.

tzn...

$\begin{pmatrix} 1 & 0 & 0 & 0 & x & x\nl 0 & 1 & 0 & 0 & x & x\nl 0 & 0 & 1 & 0 & x & x\nl 0 & 0 & 0 & 1 & x & x\nl \end{pmatrix}$

A začneme doplňovat tak třeba první řádek... Když si to nakreslím... Nakreslím si všechny vrcholy... Zakreslím hrany kostry které neodebírám tzn. v tomto případě dokreslím hrany 2, 3, 4... A vidím na jaké komponenty ten graf rozdělím.. tj... vrchol vlevo dole bude osamocen a zbytek spojen...
Pokud bych přidal hranu č. 6 ztratil bych nesouvislost takže jí musím odebrat. přidáním hrany 5 však nesouvislost zůstává... tudíž matice bude po prvním "průchodu" vypadat následovně:

$\begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 1\nl 0 & 1 & 0 & 0 & x & x\nl 0 & 0 & 1 & 0 & x & x\nl 0 & 0 & 0 & 1 & x & x\nl \end{pmatrix}$

Pokud budu postupovat dále.... opět si zakreslím všechny vrcholy a hrany patřící do kosty.. kromě hrany 2... opět vidím komponenty, které vzniknou.... (dolní spojnice) a (horní spojnice + ocásek) pokud bych neodebral hranu 5 nebo 6 ztratil bych nesouvislost... tudíž je odebrat musím a matice bude vypadat takto:

$\begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 1\nl 0 & 1 & 0 & 0 & 1 & 1\nl 0 & 0 & 1 & 0 & x & x\nl 0 & 0 & 0 & 1 & x & x\nl \end{pmatrix}$

další kroky by měli být jasné. Výsledná matice by měla vypadat takto:

$\begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 1\nl 0 & 1 & 0 & 0 & 1 & 1\nl 0 & 0 & 1 & 0 & 1 & 1\nl 0 & 0 & 0 & 1 & 0 & 0\nl \end{pmatrix}$

Což odpovídá tomu tvému řešení...

Pokud by šli vybrat nějaké další hranové řezy, tak by se dali napsat jako lineární kombinace rádků té matice...

Jinak být tebou tak si stáhnu nějaká skripta diskrétní matematiky... Npříklad Kaiser, Brousek, Ryjáček... něco takovýho

EDIT: Koukám že si tam nahoře našel "pouhým okem" ten řez {2,3}... Jak jsem již řekl musí vzniknout lineární kombinací "nějakých řádků" té matice....

takže pokud mám vybrat hranu 2 a 3.. tak musím rozhodně použít oba dva řádky... ty sečtu... a dostanu výsledný řez...

to jest vektor 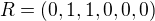$R=(0,1,1,0,0,0)$

Sčítání samozřejmě musí být modulo 2...

EDIT2:
Ty řádky jsou vždycky lineárně nezávislé... to je dané tou jednotkovou podmaticí...

Benny.RxT · 23. 06. 2010 15:34

Ok už je mi to jasný, dík

ondrej.hav

Není zač jen ještě doplním... Pokud bys chtěl prostor kružnic, dělá se to stejně... jen nejdříve očísluješ hrany mimo kostru, a jednotková podmatice bude velikosti C(cyklomatické číslo) tj (E(G)-V(G)+1) a jedničky píšeme na pozice hran, které musíme přidat aby spolu s vybranou hranou tvořily cyklus(kružnici).

Matematické Fórum

#1 22. 06. 2010 17:15

Hranové řezy

#2 22. 06. 2010 23:15 — Editoval petrkovar (22. 06. 2010 23:16)

Re: Hranové řezy

#3 22. 06. 2010 23:47 — Editoval ondrej.hav (23. 06. 2010 00:17)

Re: Hranové řezy

#4 23. 06. 2010 15:34

Re: Hranové řezy

#5 23. 06. 2010 15:58 — Editoval ondrej.hav (23. 06. 2010 18:22)

Re: Hranové řezy

Zápatí