Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 23. 06. 2010 16:56
Extrémy funkce(x,y)
Offline
#2 23. 06. 2010 17:10
Re: Extrémy funkce(x,y)
↑ Balcik:
Zakrúžkované: Nemám čo dodať, len sa to derivuje. Môžeš si prejsť metódy derivovania.
Hessova matica: Ak je pozitívne definitná v stacionárnom bode -> lokálne minimum, záporne definitná v st.b. -> lokálne maximum.
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#3 23. 06. 2010 18:37
- kaja(z_hajovny)

- Místo: Lážov
- Příspěvky: 1002
- Reputace: 12
- Web
Re: Extrémy funkce(x,y)
mozna pomuze http://user.mendelu.cz/marik/maw/index. … m=minmax3d
Offline
#4 23. 06. 2010 20:02 — Editoval ondrej.hav (23. 06. 2010 20:07)
- ondrej.hav
- Příspěvky: 162
- Reputace: 4
Re: Extrémy funkce(x,y)
↑ Balcik:To co jsi zakroužkoval jsou parciální derivace... to znamená, že derivujeme (v prvnim pripade) podle x a pak podle y... Druhou proměnnou vždy bereme jako konstantu...
Vektor, ktery obsahuje prvni parcialní derivase ce snazývy gradient....
Stacionární bod je takový pro který platí, že gradient v tomto bodě je roven nulovému vektoru...
A Hessova matice: Tak to je matice druhých parciálních derivací.... viz.: Odkaz
No a o jake druhy extremu se jedná poznáme právě z Hessovy matice, dosazením stacionárních bodů... Pak např. podle Silvestrova kritéria rozhodneme o definitnosti te formy a tím dostaneme druh dosazovaného bodu. Můžou nastat tři možnosti. Minimum, maximum a sedlo...
Pokud je pozitivně definitní tak se jedná o bod minima
Pokud je negativně definitní jedná se o bod maxima
pokud je indefinitní jedná se o sedlový bod
Pokud je jakkoli semidefinitní pak nemůžeme rozhodnout....
Offline
#6 23. 06. 2010 21:12
Re: Extrémy funkce(x,y)
↑ Balcik:
Odkiaľ si vzal ten zlomok? Príklad: Máme polynóm 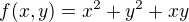 . Máme derivovať podľa x. Tak si zafixujeme premennú y a berieme ju ako číslo.
. Máme derivovať podľa x. Tak si zafixujeme premennú y a berieme ju ako číslo. 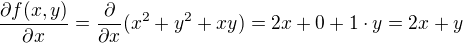
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#7 23. 06. 2010 21:38 — Editoval ondrej.hav (23. 06. 2010 21:47)
- ondrej.hav
- Příspěvky: 162
- Reputace: 4
Re: Extrémy funkce(x,y)
Celý ten zlomek to 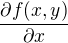 značí pouze to, že děláme parciální derivaci funkce f podle proměnné x... Jednoduše si představ (při
značí pouze to, že děláme parciální derivaci funkce f podle proměnné x... Jednoduše si představ (při 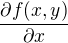 ) že y je nějaké číslo... například (8)...
) že y je nějaké číslo... například (8)...
a pokud budš mít polynom, 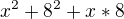 tak při derivování (klasicky podle x jak si zvyklý z funkcí jedné proměnné) budeš derivovat jako
tak při derivování (klasicky podle x jak si zvyklý z funkcí jedné proměnné) budeš derivovat jako 
a teď si představ že to číslo je to tvoje y... to znamená, že pokud derivuješ samotná y dostáváš nulu a pokud derivuješ součin y*x tak dostaneš y...
stejně jako když by si derivoval 8*x tak dostaneš 8.
Uf... polopatičtěji už to neumím...
Pak například 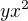 by si derivoval jako
by si derivoval jako 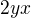 ...
...
Stejně jako  by si derivoval jako
by si derivoval jako 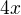 nebo rozepsané
nebo rozepsané 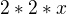
Rozumíme?
Offline
#9 23. 06. 2010 23:36 — Editoval Grein (23. 06. 2010 23:41)
Re: Extrémy funkce(x,y)
Ahoj, tady mas vyreseny kompletne cely priklad :-)
Pomoci te Hessovy matice, zjistis zda v tom Stacionarnim bode je ubec nejaky extrem, kdyz vyjde mensi jak 0, tak neni, kdyz vetsi jak 0, tak je a kdyz vyjde =0, tak nelze rozhodnout... Kdyz teda zjistis, ze tam je extrem, tak se ridis podle te druhe parcialni derivace podle x, kdyz je to mensi jak nula, tak tam je maximum a kdyz vetsi jak nula, tak je tam minimum. Doufam, ze to pochopis z meho textu :-).
Offline
#10 24. 06. 2010 00:24 — Editoval ondrej.hav (24. 06. 2010 00:27)
- ondrej.hav
- Příspěvky: 162
- Reputace: 4
Re: Extrémy funkce(x,y)
↑ Grein:
Nejdříve bych chtěl reagovat na spojení matice je < 0. Asi není od věci napsat determinant...
Možná by bylo lepší uvést Silvestrovo kritérium...
Avšak to co napsal Grein rozhodně platí. Jestliže jste si říkali něco o sedlových bodech tak ještě může nastat situace, kdy tam sice není extrém, ale sedlový bod... to znamená že v jednom směru se jedná o minimum a v druhém o maximum...
Takovou vlastnost má stacionární bod v případě že nastane jakákoli nenulová možnost, která nevyhovuje dříve uvedeným podmínkám...
Offline
#11 24. 06. 2010 10:49
Re: Extrémy funkce(x,y)
↑ Grein:, ↑ ondrej.hav:
Ahoj. Jen považuju za vhodné zmínit, že tento návod platí pouze pro funkce 2 proměnných. Obecně by to mělo být snad takto:
Hessova matice singulární - nelze rozhodnout
Pokud je regulární tak platí:
pozitivně definitní => lokální minimum
negativně definitní => lokální maximum
indefinitní => sedlový bod
Pozitivní, resp. negativní definita se dá určit pomocí Sylvestrova kritéria: matice je pozitivně definitní, pokud všechny hlavní rohové subdeterminanty jsou kladné. Pokud je první záporný a další postupně střídají znaménka, pak je matice negativně definitní. Pokud neplatí ani jedno (a Hessova matice je přitom regulární), pak je matice indefinitní.
Poprosil bych někoho zběhlejšího, aby to kdyžtak potvrdil.
Offline
#13 24. 06. 2010 15:14
- ondrej.hav
- Příspěvky: 162
- Reputace: 4
Re: Extrémy funkce(x,y)
↑ LukasM:Jasně, proto jsem psal, že by bylo vhodnější uvést Sylvestra... Nicméně pro zadání (funkce dvou proměnných) jsem souhlasil s Greinem...
P.S.: Ty jednotlivé případy definitnosti jsem už výše uvedl...
Offline
#14 24. 06. 2010 15:25
Re: Extrémy funkce(x,y)
↑ Grein:, ↑ ondrej.hav:
Já vím, však jsem nenapsal že je tam něco špatně. Jenom jsem prostě myslel, že je potřeba to zmínit, aby se autor tématu (nebo někdo jiný) nenaučil ten návod nazpaměť, a potom se divil že má písemku blbě, protože v zadání byla funkce 3 proměnných. To je celé:-)
Offline



