Matematické Fórum

adamo · 08. 06. 2010 12:19

Ahoj, potřeboval bych poradit s příkladem z Elektřiny a magnetismu. Docela mě tlačí čas a protože už nad tímhle chvilku sedím, napadlo mě, že se zeptám tady a jistě se dočkám správné odpovědi :).

Máme velký počet závitů N, navinutých v jedné vrstvě na kouli o poloměru R tak, že zcela pokrývají její povrch. Proud procházející drátem je I. Vypočítejte indukci mag pole ve středu koule. Prostě se nemůžu dopracovat ke správnému výsledku (autor uvádí $B = \frac{\mu_0 J N}{4R}$ kde teda J předpokládám, že bude hustota navinutí závitů.

Díky moc za pomoc

A.

medvidek · 28. 06. 2010 05:04

↑ adamo:

V prvním kroku je potřeba vyjít z Biotova-Savartova zákona a vypočítat (nebo se odkázat na výpočet) mag. pole na ose kruhové proudové smyčky. Tento výpočet je tzv. učebnicový, proto zde uvedu jen výsledný vztah. Odvození se snadno najde na internetu např. zde, zde, nebo zde.
$B=\frac{\mu_0I}{2}\frac{a^2}{(\sqrt{z^2+a^2})^3}$
$I$ je proud tečoucí smyčkou
$a$ je poloměr smyčky
$z$ je vzdálenost měřená na ose smyčky od středu smyčky

V druhém kroku se provede integrace příspěvků od infinitesimálních proudových smyček nacházejících se na povrchu koule o poloměru $R$ . Integrovat budeme přes úhel $\phi$ , který je svírán v centru koule mezi osou smyčky a smyčkou.
Na povrchu koule platí $R^2=a^2+z^2$ , proto můžeme psát $B=\frac{\mu_0I}{2}\frac{a^2}{R^3}$
Vzhledem k tomu, že chceme integrovat přes úhel $\phi$ , převedeme proměnnou $a$ na úhel $\phi$ .
Víme, že platí $sin \phi = \frac{a}{R}$ . Po dosazení dostaneme
$B=\frac{\mu_0I}{2R}\sin^2 \phi$ .
Nyní přejdeme k diferenciálním veličinám tím, že místo proudu $I$ zavedeme úhlovou hustotu proudu 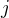$j$ (jiným slovem, kolik ampérů připadá na jeden radián na kulové sféře):
$j=\frac{NI}{\pi}$
Vyjádření v diferenciálním tvaru tedy bude
$dB=\frac{\mu_0dI}{2R}\sin^2 \phi=\frac{\mu_0jd\phi}{2R}\sin^2 \phi=\frac{\mu_0(\frac{NI}{\pi})d\phi}{2R}\sin^2 \phi$
Integrací od $0$ do $\pi$ dostaneme
$B^'=\int_0^{\pi}\frac{\mu_0NI}{2 \pi R}\sin^2 \phi \ d\phi=\frac{\mu_0NI}{2 \pi R} \ \int_0^{\pi}\sin^2 \phi \ d\phi=\frac{\mu_0NI}{2 \pi R} \cdot \frac{\pi}{2}=\frac{\mu_0NI}{4 R}$
Výsledné magnetické pole uprostřed kulové cívky je
$B^'=\frac{\mu_0NI}{4 R}$
Jak je vidět, nefiguruje zde žádná hustota proudu ani hustota navinutí závitů cívky, ale pouze počet závitů, proud tečoucí cívkou a poloměr koule.

Místo $J$ ve tvém výsledku má být zřejmě $I$ .

Matematické Fórum

#1 08. 06. 2010 12:19

Magnetická indukce od závitů na sféře

#2 28. 06. 2010 05:04

Re: Magnetická indukce od závitů na sféře

Zápatí