Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 24. 06. 2010 11:30
#5 24. 06. 2010 11:52
- Dr. Marlen
- Příspěvky: 44
- Reputace: 1
Re: komplexní čísla 2.
Anebo tu minus jedničku převedš na pravou stranu rovnice, kterou pak prostě odmocníš (třeba přes rozšířenou moivreovu větu). Třetí odmocnina z nenulového komplexního čísla má v oboru komplexních čísel 3 řešení, která budou zároveň kořeny rovnice.
Offline
#6 24. 06. 2010 12:07
#7 24. 06. 2010 12:15
- Dr. Marlen
- Příspěvky: 44
- Reputace: 1
Re: komplexní čísla 2.
Univerzální postup je, že převedeš na pravou stranu vše, kromě neznámé, a pak tu rovnici odmocníš. V prvním příkladě tedy vyjde třetí odmocnina z i, ve druhém šestá odmocnina z jedné a ve třetím čtvrtá odmocnina z (-1+i). Všechna řešení těch odmocnin pak dopočítáš tou upravenou Moivreovou větou.
Offline
#8 24. 06. 2010 12:20
Offline
#9 24. 06. 2010 12:28
Offline
#10 24. 06. 2010 12:33
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: komplexní čísla 2.
↑ zdenek1:
Ahoj, děkuji. Mohla bych tě poprosit o vysvětlení 1, tak aby mě to vyšlo v sin a cos?
Offline
#11 24. 06. 2010 12:47
Re: komplexní čísla 2.
↑ Lucinecka88:
Vyjádříš si obě čísla v goniometrickém tvaru ,
, 
Rovnice je pak
takže a ,
a , 
 ,
, 






Pořádek je pro blbce, inteligent zvládá chaos!
Offline


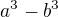 a vyjde ti jeden reálný kořen a dva z oboru komplexních čísel
a vyjde ti jeden reálný kořen a dva z oboru komplexních čísel





 nebo
nebo 











