Matematické Fórum

CzechMan

Omlouvám se až edukativní charakter tohoto topicu, bohužel odráží mé myšlenky :).

Dávno tomu, bylo mi zde doporučeno se naučit integrovat. Konečně jsem se k tomu dopracoval ..a tak trochu pochopil, ale vyvstaly další otázky.
Nejvíce mě zajímala aplikace určitého integrálu pro výpočet obsahů a objemů. Pro to mi stačila Leibniz-Newtonova formule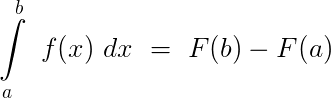
$\Large\int\limits_{a}^b~f(x)\ dx \ =\ F(b)-F(a)$
Sice vztah umím používat, ale nechápu jej :). Všude, kde jsem se tomuto snažil přijít na kloub, to vypadalo asi takto:

Rozřezání grafu v intervalu <a,b> --> zavedení pojmů dolní/horní integrační součet --> limitovaný integrační součet najednou značíme jako určitý integrál --> Newtonův integrál.

Snad chápete můj problém. Ze všech možných obrázků, atd. jsem nepřišel na žádný vztah mezi integračním součtem fce v intervalu a rozdílem hodnot primitivní fce v krajních bodech intervalu.

Nevím, zda je to natolik zřejmé (a já blbec) nebo prostě natolik složité, že vysvětlení je potřeba hledat hlouběji.

Byl bych moc rád za osvětlení :))

Kondr · 16. 09. 2007 22:28

limitovaný integrační součet najednou značíme jako určitý integrál

limitovaný integrační součet je roven Riemanově integrálu (R. integrál je definován jako tento součet). Ten se za určitých podmínek rovná Newtonově intgrálu (ten je definován jakorozdíl primitivní funkce k f na začátku a na konci intervalu).
Každdý z těchto integrálů (je-li definován) je roven ploše pod křivkou na intervalu <a,b>. U Riemanova integrálu je to zřejmé. U Newtonova integrálu je to složitější: Uvažme funkci G(x), která udává plochu pod křivkou f na intervalu <a,x>. Nyní hledejme derivaci funkce f. Tu najdeme z definice jako 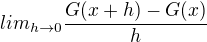$lim_{h\rightarrow0}\frac{G(x+h)-G(x)}{h}$ . Rozdíl ve jmenovateli je rozdíem mezi obsahy pod křivkou
na intervalech <a,x+h> a <a,x>. Tento rozdíl je obsahem pod křivkou na intervalu <x,x+h>. Pokud se nebudeme zabývat formalismy, můžeme říct, že f(x) je na tomto intervalu konstatní (na nekonečně krátkém intervalu se nemůže změnit, když stoupá konečně rychle*). Plocha na tomto intervalu je proto h.f(x), derivace funkce G je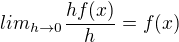
$lim_{h\rightarrow0}\frac{hf(x)}{h}=f(x)$ . G(x) je proto primitivní funkcí k f(x). Nevíme sice jakou, ale náš hledaný obsah je roven G(b)=G(b)-G(a)=F(b)-F(a), kde F je libovolná primitivní fce.

Lishaak · 17. 09. 2007 10:17

Tak Kondr to tady suprově formálně vystihl, takže já bych si k tomu dovolil jenom přidat takovou tu pohádku pro lidi, kteří by se v těch vzorcích neradi utopili.

Klíčovým poznatkem ohledně určitých integrálů je toto:

Mějme nějakou funkci f(x) pro jednoduchost kladnou a spojitou na intervalu <a,b>. Zvolme si bod x tak, že leží mezi body a, b a podívejme se na obsah plochy pod křivkou na intervalu <a,x>. Toto číslo udávájící onen obash si označme V(x). Vidíme jasně, že číslo V(x) se mění podle toho, kam mezi body a, b ono x umístíme. Tedy řekneme, že V(x) je funkce proměnné x.

A teď přichází ta bomba. Stačí si totiž uvědomit (viz. Kondrův příspěvek), že funkce f(x) je derivací funkce V(x) (mně osobně to přijde celkem zajímavé, že to takhle platí). No a teď už jsme za vodou, nebo? abychom našli funkci, která říká jak rychle se mění obsah pod křivkou f(x), stačí najít funkci F(x), pro kterou platí, F '(x) = f(x)

Důležité je uvědmit si, že funkce F(X) vyjadřuje pouze to, jak rychle se ten osbah mění, nikoliv samotné hodnoty tohoto obahu. To proto, že funkcí F(x), pro které platí F '(x) = f(x) je nekonečně mnoho, ale všechny mají stejnou derivaci, tedy jakoby stejný průběh.

Teď už je snadné si uvědomit, proč rozdíl hodot F(b) - F(a) dává obsah pod křivkou f(x) na intervalu <a,b>

CzechMan · 17. 09. 2007 21:49

Super! Děkuji vám oboum.

Obviňuji Newtona z toho, že na tento vztah přišel pouhou náhodou! Když jsem si vysvětlení četl, zůstal jsem v úžasu rozhodně větším nežli po představení Copperfielda a Derrena Browna zároveň :)

Kondr · 17. 09. 2007 22:15

Fakt je, že za Newtona byla matematika daleko intuitivnější. Zápis s limitou pokud vím korektně zavedl až Cauchy o sto let později. Newton pracoval spíš s geometrickou představou a hlavně s veličinami jako rychlost, zrychlení, dráha, které umožňují lepší představu.

Lishaak · 17. 09. 2007 23:08

Je to tak, nebot newton byl predevsim fyzik, cili se mu tyhle jeho derivace nadherne hodily do kramu. Ale prave kvuli tomu ze nemel potrebny formalni zaklad tak to vsechno byla takova docela magie. Byli i hlasy, ktere newtona ve sve dobe velmi kritizovaly za to, ze je ta jeho teorie cela takova samanska. A prave to byl newton, kdo se pri obhajobe pred temito odpurci uz temer dotkl pojmu limita. Ale nakonec na nej nedosahl a tak az do doby, kdy d'Alembert zavedl limity a Cauchy je pak vyuzil k formalizaci infinitezimalniho poctu, vsichni videli, ze infinitezimalni pocet funguje a fyzici z toho hodne tezili ale vlastne nikdo nevedel proc to vsechno funguje. Sto let tomu proste vsichni verili tak rikajic "bez dukazu"

Matematické Fórum

#1 16. 09. 2007 20:49 — Editoval CzechMan (16. 09. 2007 20:50)

Určitý integrál

#2 16. 09. 2007 22:28

Re: Určitý integrál

#3 17. 09. 2007 10:17

Re: Určitý integrál

#4 17. 09. 2007 21:49

Re: Určitý integrál

#5 17. 09. 2007 22:15

Re: Určitý integrál

#6 17. 09. 2007 23:08

Re: Určitý integrál

Zápatí