Matematické Fórum

nika.v · 01. 04. 2008 13:07 — Editoval nika.v (01. 04. 2008 13:14)

lim n jde k oo, zlomku, kde čitatal jest (2n+1)na3-(2n-1) a jmenovatel 3nna2

už jsem z toho jelen

Lishaak · 01. 04. 2008 19:57

Jestli je to mysleno takto: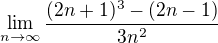

$\lim_{n\to\infty}\frac{(2n+1)^3-(2n-1)}{3n^2}$

Tak to staci nahore roznasobit a neni problem. Pokud je clovek zkusenejsi, ihned si uvedomi, ze stupen citatele je vetsi nez stupen jmenovatele a tedy je ta limita nekonecno.

nika.v · 03. 04. 2008 07:35

↑ Lishaak:

Ahojky, ty úpravy jsem způsobila :-), ale stále mi vychází 8/0, tak nevím a zoufám si. Kdyby mi vycházelo 8/n, tak je zřejmé, že se blíží k 0. Vysvětlito jelitu, prosím?! Děkuju.

jelena · 03. 04. 2008 08:36 — Editoval jelena (03. 04. 2008 08:56)

↑ nika.v:

Troufnu si zopakovat svuj polopaticky vyklad :-)

Deleni nenulového cisla nulou - mam 8 jablek a nebudu se s nikym delit - mam nekonecny pozitek z techto jablek.

8/0 = oo

Deleni nenuloveho cisla nekonecnem - mam 8 jablek a budu se delit s nekocne velkym poctem kamaradu - kazdy dostane nekonecne maly kousek, tedy 8/oo je 0.

Odborne rady se snad take dostavi :-)

Editace: osobne bych v tomto pripade radej pouzila pomucku o pomeru nejvyssich mocnin v citateli a v jmenovateli - kdo vi, jak bych otevrela zavorky:-)

Lishaak · 03. 04. 2008 10:05

$\lim_{n\to\infty}\frac{(2n+1)^3-(2n-1)}{3n^2}=\lim_{n\to\infty}\frac{8n^3 + 12n^2 + 4n + 2}{3n^2} = \lim_{n\to\infty}\left(\frac{8n^3}{3n^2} + \frac{12n^2}{3n^2} + \frac{4n}{3n^2} + \frac{2}{3n^2}\right) = \nl \lim_{n\to\infty}\left(\frac{8}{3}n + 4 + \frac{4}{3n} + \frac{2}{3n^2}\right) = \infty + 4 + 0 + 0 = \infty$

Matematické Fórum

#1 01. 04. 2008 13:07 — Editoval nika.v (01. 04. 2008 13:14)

Limita posloupnosti

#2 01. 04. 2008 19:57

Re: Limita posloupnosti

#3 03. 04. 2008 07:35

Re: Limita posloupnosti

#4 03. 04. 2008 08:36 — Editoval jelena (03. 04. 2008 08:56)

Re: Limita posloupnosti

#5 03. 04. 2008 10:05

Re: Limita posloupnosti

Zápatí