Matematické Fórum

raymond · 06. 07. 2010 18:27

Mohl by mi prosím někdo poradit co s tímto příkladem, m ám určit vázané extrémy na množině M: y- 2x = 0

$f(x,y)=e^(xy-4x)$

po první derivaci mi vyšlo že x=1 y=2,

což je zřejmě špatně protože jejich součet by měl dávát dohromady 1 , nevíte někdo?

stenly · 06. 07. 2010 19:15

↑ raymond:Máš to dobře.Vazbu y=2x si dosaď do funkce a derivuj dle x,dostaneš y´=e^(2x^2-4)*(4x-4)=0 a z toho x=1 ,dosadíš do vazby a máš y=2.Postup je pak jednoduchý,provedeš druhou derivaci a pokud je menší než nula v daném bodě,pak je tam maximum a naopak.

99 · 06. 07. 2010 19:23

↑ raymond:

jde to i přes druhou derivaci f'xx

raymond · 06. 07. 2010 19:23

↑ stenly:díky moc =)

raymond · 06. 07. 2010 19:35

a ještě když mám zjistit vázaný extrém na fci: f(x,y)=x-y na množině $x^2+y^2-2=0$

mohla bych to počitat přes jakobiána, to mi totiž vyšlo $x=-y$ a $y^4=2$

což je asi špatně že?

Olin · 06. 07. 2010 19:37 — Editoval Olin (06. 07. 2010 23:59)

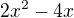Jde to i mnohem snáz, stačí si uvědomit, že v reálných číslech je $\mathrm{e}^z$ rostoucí funkce, takže $\mathrm{e}^{xy-4x}$ bude mít extrémy přesně tam, kde bude mít extrémy i $xy-4x$ . Pak už jen dosadíme $y = 2x$ a vyšetřujeme, kde má extrémy kvadratická funkce $2x^2-4x$ , což je již triviální doplněním na čtverec $2x^2-4x = 2(x-1)^2 - 2$ .

Olin · 06. 07. 2010 20:22 — Editoval Olin (06. 07. 2010 23:53)

K tomu druhému: já jakobínům a těmto věcem okolo moc nerozumím, takže jen navrhnu alternativní řešení. První se zakládá na tom, že si zadanou množinu (kružnici) rozdělíme na část, kde $y \geq 0$ , a kde $y < 0$ . V prvním případě je $y = \sqrt{2-x^2}$ (pak je $f(x, y) = x-\sqrt{2-x^2}$ ) a v druhém je $y = -\sqrt{2-x^2}$ (pak je $f(x, y) = x+\sqrt{2-x^2}$ ). U obou výrazů najdeme extrémy derivováním podle x.

Druhé řešení se zakládá na tom, že jelikož vyšetřujeme body na kružnici, můžeme si je snadno vyjádřit jako $x = \sqrt{2} \cos \varphi,\, y = \sqrt{2} \sin \varphi,\, \varphi \in [0,\, 2\pi]$ . Pak stačí jen nalézt extrém funkce $\sqrt{2} $ \cos \varphi - \sin \varphi $$ , což se dá třeba derivovat, nebo upravit na tvar $-2 \sin $\varphi - \frac{\pi}{4}$$ , ze kterého je již vše patrné.

EDIT: Ještě mě napadl třetí způsob. Zavedením nových souřadnic $\tilde{x} = \frac{x}{\sqrt{2}} + \frac{y}{\sqrt{2}},\, \tilde{y} = \frac{x}{\sqrt{2}} - \frac{y}{\sqrt{2}}$ se nám množina prakticky nezmění (bude dána rovnicí $\tilde{x}^2 + \tilde{y}^2 - 2 = 0$ ) a funkce dostane tvar $f(\tilde{x}, \tilde{y}) = \sqrt{2}\tilde{y}$ . U takovéto funkce se již extrémy nachází opravdu snadno - prostě se snažíme mít souřadnici $\tilde{y}$ co největší/nejmenší. To nastane zřejmě v případech $\tilde{y} = \pm \sqrt{2}$ , tedy $\tilde{x} = 0$ .

Nevím ale, jestli ti tato řešení na něco budou, a tak raději počkejme na někoho z kolegů.

Rumburak

↑ raymond:
Máš pravdu, to " $y^4=2$ " je zde vskutku špatně :-).

Když $x=-y$ dosadím do vazby $x^2+y^2-2=0$ , tak dostanu $x^2=y^2=1$ .

↑ Olin: Podmínka D = 0 , kde D je jakobián zúčastněných funkcí, je ekvivalentní s podmínkou existence Lagrangeova multiplikátoru ze známé věty.

Matematické Fórum

#1 06. 07. 2010 18:27

Vázanéé extrémy

#2 06. 07. 2010 19:15

Re: Vázanéé extrémy

#3 06. 07. 2010 19:23

Re: Vázanéé extrémy

#4 06. 07. 2010 19:23

Re: Vázanéé extrémy

#5 06. 07. 2010 19:35

Re: Vázanéé extrémy

#6 06. 07. 2010 19:37 — Editoval Olin (06. 07. 2010 23:59)

Re: Vázanéé extrémy

#7 06. 07. 2010 20:22 — Editoval Olin (06. 07. 2010 23:53)

Re: Vázanéé extrémy

#8 07. 07. 2010 09:09 — Editoval Rumburak (07. 07. 2010 09:16)

Re: Vázanéé extrémy

Zápatí