Matematické Fórum

Noifernus · 02. 07. 2010 21:05

Jak by se počítal příklad: Najděte absolutní extrémy na funkci f(x,y,z)=1+z+x+y^2 na množině x^2+y^2+z^2<=4 ?Lokální extrémy bych věděl jak spočítat,ale absolutní nevím.

kaja(z_hajovny) · 02. 07. 2010 21:40

najde se vazany extrem na hranici a porovna se s tim lokalnim uvnitr.

Noifernus · 02. 07. 2010 21:47

↑ kaja(z_hajovny):Takže vypočítám 1+z+x+y^2+lambda*(x^2+y^2+z^2-4)? Vypočítam prvni derivace podle x,y,z + rovnice x^2+y^2+z^2-4 a soustavu 4 rovnic o 4 neznámých vyřeším?..vyjdou mi stacionarní body.Je tento postup spravne?

fl4sk4 · 03. 07. 2010 18:11

Najít extrémy $f(x,y,z)=1+z+x+y^2$ na množině $x^2+y^2+z^2<=4$

a) Najdeme lokální extrémy $f(x,y,z)=1+z+x+y^2$ na množině $x^2+y^2+z^2=4$
Úlohu převedeme na hledání lokálních extrémů funkce:
$\Lambda(x,y,z) = 1 + z + x + y^2 - \alpha(x^2 + y^2 + z^2 - 4)$
Za dodatečných podmínek:
$x^2+y^2+z^2=4$

a) Najdeme lokální extrémy $f(x,y,z)=1+z+x+y^2$ všude, ale vezmeme v potaz jen ty na množině: $x^2+y^2+z^2<4$

c) Obě množiny bodů pak mezi sebou porovnáme a najdeme tak globální extrém funkce na množině: $x^2+y^2+z^2<=4$

Noifernus · 03. 07. 2010 18:19

$\Lambda(x,y,z) = 1 + z + x + y^2 - \alpha(x^2 + y^2 + z^2 - 4)$ sestavil jsem rovnice prvních derivací, ale ani za boha nemůžu vyjádřit vyřešit tu soustavu.

df/dx 1+2*a*x = 0
df/dy 2*y+*2*a*y = 0
df/dz 1+2*a*z = 0
x^2+y^2+z^2 = 4

Poradíte mi?

fl4sk4 · 03. 07. 2010 18:27 — Editoval fl4sk4 (03. 07. 2010 18:28)

$\frac{\partial \Lambda(x,y,z)}{\partial x} = 1-2ax = 0\nl \frac{\partial \Lambda(x,y,z)}{\partial y} = 2y-2ay = 0\nl \frac{\partial \Lambda(x,y,z)}{\partial z} = 1-2az = 0\nl x^2+y^2+z^2 = 4$

$x=\frac{1}{2a}\nl y=0\nl z=\frac{1}{2a}\nl x^2+y^2+z^2 = 4$

$\frac{1}{4a^2}+\frac{1}{4a^2} = 4$

$\frac{2}{4a^2} = 4$

$a=\pm\frac{1}{\sqrt[2]{8}}$

$x=\frac{\pm \sqrt[2]{8}}{2}\nl y=0\nl z=\frac{\pm \sqrt[2]{8}}{2}\nl$

Noifernus · 03. 07. 2010 18:47

↑ fl4sk4: Takže mám 4 body podezřelé z extrému?Lokální extrémy nemá funkce 1+z+x+y^2 žádné, budou to tedy body co vyšli při vázaném extrému.Pomocí Sylvestrova kritéria zjistím extrémy a největsí maximum bude absolutní maximum a nejmenší minimum bude absolutní minimum.Je to tak?

Noifernus · 03. 07. 2010 19:00

↑ fl4sk4:IOprava..jen dva podezřelé body.A[8^0.5/2; 0; 8^0.5/2] a B [-8^0.5/2; 0; -8^0.5/2].Přičemž v bodě A extrém nenastáva a v bodě B je pak absolutní minimum.Mám to správně?

Wyler · 04. 07. 2010 13:13

↑ Noifernus:

V ty LaGrangove funkci tu druhou funkci (vazbu nasobenou multiplikatorem) odcitate. Ja vzdy myslel ze se ma pricitat.

fl4sk4 · 04. 07. 2010 14:08

↑ Noifernus: Ano jsou to dva body. Existenci extrému je třeba ještě, jak správně říkáš, ověřit Sylvestrovým kritériem.
↑ Wyler: Je to jedno, zda tu funkci přičítáš, či odčítáš. LaGrangeovy multiplikátory se pak budou lišit až na znaménko. Já jsem zvyklý ji odčítat, jelikož když tu větu o nutné podmínce extrému na varietě dokazuješ, je logičtější to odčítat, ale je to jedno.

Noifernus

↑ fl4sk4:Opravdu jsou řešením jen dva body?Učitel mi příklad vrátil s tím že nemám nalezené všechny body podezřelé z extrému. Lokální extrém podle mě funkce nemá a z vázaného extrému vyplynuly dva body. Jak mám najít další? Už se v tom trošku ztrácím.

jelena · 05. 07. 2010 20:46

↑ Noifernus:

Zdravím, pokud dotaz navazuje na řešení od kolegy ↑ fl4sk4:, tak má 4 body podezřelé z extrému:

Využito zápisu kolegy, dškuji.

jeden $x=\frac{\sqrt[2]{8}}{2}\nly=0\nlz=\frac{\sqrt[2]{8}}{2}$ , druhý $x=\frac{-\sqrt[2]{8}}{2}\nly=0\nlz=\frac{\sqrt[2]{8}}{2}$

třetí $x=\frac{\sqrt[2]{8}}{2}\nly=0\nlz=\frac{-\sqrt[2]{8}}{2}$ čtvrtý $x=\frac{- \sqrt[2]{8}}{2}\nly=0\nlz=\frac{- \sqrt[2]{8}}{2}$

Uvnitř množiny mi žádný podezřelý nevyšel, ale jsem to spočetla jsem "zběžně". V pořádku?

Noifernus · 06. 07. 2010 09:39

↑ jelena:Bod $x=\frac{\sqrt[2]{8}}{2}\nly=0\nlz=\frac{\sqrt[2]{8}}{2}$ a bod $x=\frac{- \sqrt[2]{8}}{2}\nly=0\nlz=\frac{- \sqrt[2]{8}}{2}$ jsou mi jasn7 jak se k nim dostat.Ale body $x=\frac{-\sqrt[2]{8}}{2}\nly=0\nlz=\frac{\sqrt[2]{8}}{2}$ a $x=\frac{\sqrt[2]{8}}{2}\nly=0\nlz=\frac{-\sqrt[2]{8}}{2}$ netuším.Protože když dosadím $a=\pm\frac{1}{\sqrt[2]{8}}$ za alfa jednou + jednou - do výrazů x,y $x=\frac{1}{2a}\nly=0\nlz=\frac{1}{2a}\nlx^2+y^2+z^2 = 4$ tak mi přeci nemůžou výjít tyhle dvě další kombinace,nebo ano?

jelena · 06. 07. 2010 09:51

↑ Noifernus:

použila jsem zápis výsledků, jak má kolega ↑ fl4sk4: v příspěvku 6.

Ovšem, když se dívám na postup od kolegy, tak bych postupovala ještě jinak. Kořeny, jak našel a jak jsi sestavil - 2 kořeny to je v pořádku, ale vynechal jedno řešení:

z rovnice $2y-2ya=0$ plyne $y(2-2a)=0$ , tedy rovnice platí pro $y=0$ nebo pro pro každé y z R, pokud a=1.

Odsud jsou další kořeny. Dosazením a=1 do zbývajících rovnic pro x a pro z.

Snad alespoň tak v náznaku.

Noifernus

↑ jelena:Takže pokud to chápu dobře,tak kromě 2 již výše zmíněných kořenech zde bude ješte jeden kořen a to když 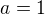$a=1$ .Souřadnice bodu y pak musí splnovat rovnici $x^2+y^2+z^2=4$ ,takže zbývající podezřelý bod bude [1/2, 7/2 , 1/2]. Žádný další bod už nebude.Souhlasíte?

jelena · 06. 07. 2010 10:45

↑ Noifernus:

neúplně:

$\frac14+\boxed{y^2}+\frac14=4$ , odsud máme 2 různé hodnoty y - je to tak?

Tedy z teto rovnice jsou dalsi 2 koreny.

Noifernus · 06. 07. 2010 11:06

↑ jelena:Máte pravdu.2 kořeny.Děkuji

Noifernus

↑ jelena:Sylvestrovo kritérium pro alfa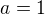 $a=1$ selhává D2=0 a D3=0.Je závěr takový, že v bode není extrém nebo je nutno použít jiné kritérium prípadně jaké?Je nutno vůbec v tomto případě použít Sylvestrovo kritérium, nestačí dosadit podezřelé body do $f(x,y,z)=1+z+x+y^2$ zjistit funkční hodnoty a prohlasit největší výsledek za absolutní maximum a nejmenší hodnotu za absolutní minimum?

jelena · 06. 07. 2010 15:41

↑ Noifernus:

já se omlouvám, momentálně mám jiné aktivity a nemohu překontrolovat, zda vychází nebo nevychází (bude věřit tomu, co vyšlo), potom je možné použit i jiných nástrojů - viz například zde - ve studijním textu.

podle strojového výpočtu to vychází tak - viz odkaz - co se tyče samotných podezřelých bodů, to sedi

Zda to jde jen dosadit, bez ověřování, to nejsem tak úplně jista - snad někdo z kolegů doplní, děkuji.

Noifernus · 06. 07. 2010 17:02

↑ jelena:Body vychází, ale jak mám dokázat že tam je maximum,když Sylvestrovo kritérium selže. V tom studijním textu žadný popis jak to zjistit není.

99 · 06. 07. 2010 19:08

↑ Noifernus:
musí se rozhodnout podle definice !!

Definice:

Pokud v okolí bodu [x0,y0] platí f(x0,y0) \geq f(x,y) a současně g(x0,y0) = 0, pak se v bodě [x0,y0] nachází vázané lokální maximum funkce f. Pokud v okolí bodu [x0,y0] platí f(x_0,y_0) \leq f(x,y) a současně g(x0,y0) = 0, pak se v bodě [x0,y0] nachází vázané lokální minimum funkce f. Tyto body představují vázané lokální extrémy funkce f.

Jsou-li uvedené nerovnosti v okolí bodu [x0,y0] ostré, tzn. f(x0,y0) > f(x,y), resp. f(x0,y0) < f(x,y), pak hovoříme o ostrém vázaném lokálním extrému, tedy o ostrém vázaném lokálním maximu, resp. ostrém vázaném lokálním minimu.

Pokud uvedené podmínky platí nejen v okolí bodu [x0,y0], ale v celém definičním oboru funkce, pak hovoříme o globálním vázaném extrému, tedy o globálním vázaném maximu nebo globálním vázaném minimu.

by http://cs.wikipedia.org/wiki/V%C3%A1zan … xtr%C3%A9m

Rumburak

↑ Noifernus:
Množina K, na níž absolutní extrémy funkce f hledáme, je kompaktní a funkce f je na ní spojitá, proto oba hledané absoluní extrémy nutně existují.
Stačí tedy vzít všechny podezřelé body uvnitř množiny K i na její hranici a porovnat, ve kterém z nich je funkční hodnota největší resp. nejmenší
(v jiných než těchto bodech absolutní extrémy být nemohou). Sylvestrovo kriterium tedy vůbec nepotřebujeme.

Noifernus · 08. 07. 2010 12:47

↑ Rumburak:Děkuji.Už je to jasné.

Matematické Fórum

#1 02. 07. 2010 21:05

Absolutní extrémy fce 3 proměných

#2 02. 07. 2010 21:40

Re: Absolutní extrémy fce 3 proměných

#3 02. 07. 2010 21:47

Re: Absolutní extrémy fce 3 proměných

#4 03. 07. 2010 18:11

Re: Absolutní extrémy fce 3 proměných

#5 03. 07. 2010 18:19

Re: Absolutní extrémy fce 3 proměných

#6 03. 07. 2010 18:27 — Editoval fl4sk4 (03. 07. 2010 18:28)

Re: Absolutní extrémy fce 3 proměných

#7 03. 07. 2010 18:47

Re: Absolutní extrémy fce 3 proměných

#8 03. 07. 2010 19:00

Re: Absolutní extrémy fce 3 proměných

#9 04. 07. 2010 13:13

Re: Absolutní extrémy fce 3 proměných

#10 04. 07. 2010 14:08

Re: Absolutní extrémy fce 3 proměných

#11 04. 07. 2010 20:06 — Editoval Noifernus (04. 07. 2010 20:58)

Re: Absolutní extrémy fce 3 proměných

#12 05. 07. 2010 20:46

Re: Absolutní extrémy fce 3 proměných

#13 06. 07. 2010 09:39

Re: Absolutní extrémy fce 3 proměných

#14 06. 07. 2010 09:51

Re: Absolutní extrémy fce 3 proměných

#15 06. 07. 2010 10:23 — Editoval Noifernus (06. 07. 2010 10:41)

Re: Absolutní extrémy fce 3 proměných

#16 06. 07. 2010 10:45

Re: Absolutní extrémy fce 3 proměných

#17 06. 07. 2010 11:06

Re: Absolutní extrémy fce 3 proměných

#18 06. 07. 2010 12:27 — Editoval Noifernus (06. 07. 2010 12:31)

Re: Absolutní extrémy fce 3 proměných

#19 06. 07. 2010 15:41

Re: Absolutní extrémy fce 3 proměných

#20 06. 07. 2010 17:02

Re: Absolutní extrémy fce 3 proměných

#21 06. 07. 2010 19:08

Re: Absolutní extrémy fce 3 proměných

#22 07. 07. 2010 10:07 — Editoval Rumburak (07. 07. 2010 10:09)

Re: Absolutní extrémy fce 3 proměných

#23 08. 07. 2010 12:47

Re: Absolutní extrémy fce 3 proměných

Zápatí