Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy ze základní školy
- » Výpočet bez pomocí strojů - z Východu (TOTO TÉMA JE VYŘEŠENÉ)
#1 30. 06. 2010 22:25
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Výpočet bez pomocí strojů - z Východu
Zdravím vás,
v této sekci obvykle ani nepřispívám, natož zakládat témata.
Ovšem zde v tématu VŠ se kolega domnívá, že problém převodu na úplný čtverec u studenta VŠ vyřešíme tak, že doporučíme studovat EN Wikipedii i s obrázky. I to je cesta... Také mám jeden obrázek - v dotyčném tématu by to bylo OT a zbytečné zatěžování přemírou informace, tak to umístím zde.
Úkolem je navrhnout pro úlohu na tabuli metodu výpočtu bez použití žádné techniky - viz obráz. Na mém monitoru je úloha čítelná dobře, pokud bude problém se čtením, úlohu přepíší sem.
Speciální bonus - určit autora obrázu, název a rok, kdy byl namalován.
Děkuji a hodně zdaru. Jelena
Offline
- (téma jako vyřešené označil(a) jelena)
#2 30. 06. 2010 23:10 — Editoval Spybot (15. 08. 2010 20:34)
Re: Výpočet bez pomocí strojů - z Východu
Tak, odpoviem zatial aspon na druhu cast :-)
Offline
#3 30. 06. 2010 23:14
Re: Výpočet bez pomocí strojů - z Východu
První, co mě napadlo, bylo
pak jsem si ale uvědomil, že
Offline
#4 30. 06. 2010 23:17
Re: Výpočet bez pomocí strojů - z Východu
No prvé čo ma napadlo je toto:
Dalo by sa ešte aj:
Do you follow my way? Or you just see a black stain swimming in the Milky Way ...
KSP je určený pre študentov základných a stredných škôl, ktorí majú záujem naučiť sa niečo z oblasti algoritmov, logických úloh, programovania a informatiky.
Offline
#5 01. 07. 2010 00:03 — Editoval Spybot (01. 07. 2010 00:08)
Re: Výpočet bez pomocí strojů - z Východu
Tak, da sa:
No hodilo by sa upresnit zadanie. Co presne je "povolene" a co nie, tiez si tieto "zakladne" mocniny pamatam a tazko sa mi od toho odputava. Navyse, isto by sa nasli zakladoskolski "nadsenci", co by to spocitali aj z hlavy.
Offline
#6 01. 07. 2010 00:11
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Výpočet bez pomocí strojů - z Východu
Já jsem postupoval takto:
Offline
#7 01. 07. 2010 00:27
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Výpočet bez pomocí strojů - z Východu
Děkuji za návrhy :-)
↑ Spybot: ano
↑ Olin:, ↑ BrozekP: i tak, ovšem pro vás "sa posnaž o riešenie viac" (c):
↑ pizet: ano, 2. varianta řešení odpovídá postupu, který u žáků věsnické školy prosazoval učitel Račinskij.
Zjednodušenou variantu této úlohy můžete najit v knizě Perelman "Zajímavá algebra".
Varianty řešení od čtenářů časopisu Věda a život (Наука и жизнь)>
Pokud nezapomenu, tak přidám další varianty této úlohy.
Offline
#8 01. 07. 2010 00:34
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Výpočet bez pomocí strojů - z Východu
Offline
#9 01. 07. 2010 00:41 — Editoval jelena (01. 07. 2010 00:47)
#10 01. 07. 2010 00:43
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Výpočet bez pomocí strojů - z Východu
↑ jelena:
Nechal bych vysvětlení na pizetovi. :-)
Offline
#11 01. 07. 2010 07:39 — Editoval pizet (01. 07. 2010 08:09)
Re: Výpočet bez pomocí strojů - z Východu
No ja som tú rovnosť zohnal náhodne... nevedel som o tej postupnosti Račinského. Jednoducho som to umocňoval a spočítaval a nejak som si to potom z toho uvedomil, že tam platí hento.
A mimochodom, naozaj to sedí( Račinského postupnosť)?
Do you follow my way? Or you just see a black stain swimming in the Milky Way ...
KSP je určený pre študentov základných a stredných škôl, ktorí majú záujem naučiť sa niečo z oblasti algoritmov, logických úloh, programovania a informatiky.
Offline
#12 01. 07. 2010 09:02
#13 01. 07. 2010 09:45 — Editoval jelena (14. 07. 2010 17:55)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Výpočet bez pomocí strojů - z Východu
Pro kolegy - svůj cíl "reagovat na úpravu na čtverec, neproveditelnou pro studenta VŠ" jsem splnila. Jinak, jak víte, tato sekce je pro mne zakázané území, jelikož na řešení úloh v této sekci nemám potenciál.
Tak vás s důvěrou přenechám dohledu kolegy PavlaB, příadně sem doplním materiály z ruských zdrojů.
Pro milého kolegu Ondřeje - můžeš se přidat k týmu, co se má posnažit více (údajně je vyžadována nějaká znalost mimo SŠ), ale jak pozoruji příspěvký našich "mladších" kolegů v této sekci, tak usuzuji, že jejich znalosti značně převyšuji požadavky SŠ.
Všem děkuji a hezký den :-)
------------
"Z toho, co vidim a rozeznam na monitoru, se domnivam, ze se jedna o posloupnost, jejiz n-ty clen je dan vztahem..."(c)
Offline
#14 01. 07. 2010 09:56
Re: Výpočet bez pomocí strojů - z Východu
↑ jelena:
Aha ďakujem za objasnenie :).
Do you follow my way? Or you just see a black stain swimming in the Milky Way ...
KSP je určený pre študentov základných a stredných škôl, ktorí majú záujem naučiť sa niečo z oblasti algoritmov, logických úloh, programovania a informatiky.
Offline
#15 14. 07. 2010 17:54
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Výpočet bez pomocí strojů - z Východu
Zdravím vás a děkuji za řešení a poznámky. V rámci úklidových aktivit se pokusím označit téma za vyřešené:
1) kolega ↑ Spybot: správně určil údaje o obrázu,
2) úloha je formulována velmi volně. Jelikož původní úloha je z konkrétního obrázu a navazuje na konkrétní osobu - učitel Рачинский, tak bych vyhodnotila úlohu za vyřešenou, pokud bude maximálně vycházet z úvodního obrázu.
Z tohoto pohledu nejblíž obrázu se dostavají kolegové ↑ Spybot: a ↑ pizet:.
Podle materiálů pan učitel Рачинский používal (nevím, zda přímo objevil) vlastnost konečné řady po sobě jdoucích přirozených čísel, počet čísel má být lichý. V tomto případě existuje pouze jedna posloupnost, která splňuje vlastnost, že součet čtverců "prvních čísel" je stejný jako součet čtverců "posledních čísel". Počet "prvních čísel" má být o jedno větší, než počet "posledních čísel".
Podúlohy jsou:
- najdete posloupnost Račinského pro různé liché počty čísel v posloupnosti (např. pro 3, 5 (to je v úloze), 7 členů)
- obecně dokážte, že pro libovolný lichý počet po sobě jdoucích čísel lze nalezt pouze jednu posloupnost přirozených čísel, která bude splňovat vlastnost Račinského.
Definice: posloupnosti Račinského, odpovídající celému číslu k≥ 1, nazvéme řadu z (2k+1) čísel n, n+1, n+2... n+k, n+k+1... n+2к... splňujcích rovnost:(1)
Dokážte, že pro zadané celé k ≥ 1 existuje pouze jedna posloupnost Račinského.
Návrh kolegy ↑ BrozekP: ruským časopisem byl vyhodnocen jako jeden z nejvíce racionálních.
Můj postup - souhlasím s kolegou ↑ Olinem:, jsou to 2. mocniny čísel do 20, které umíme zpamětí, při součtu bych postupovala "výhodně" (121+169 apod.), ale nic jiného bych nepoužila.
Sbírku učitele Рачинского pro cvičení výpočtů zpamětí můžete najit zde: http://www.gutenberg.org/files/16527/16 … 6527-h.htm Ale sama mám problém s převodem starých jednotek. Ovšem pokud bude zájem nebo dostanu pokynem..
--------------------
"Obrázek se bude obecně kreslit hůře..."(c) ...ничего, что мы чужие, Вы рисуйте. Я потом, что непонятно, объясню...
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy ze základní školy
- » Výpočet bez pomocí strojů - z Východu (TOTO TÉMA JE VYŘEŠENÉ)
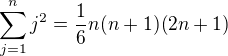 ,
,
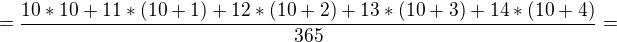


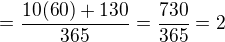
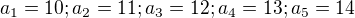
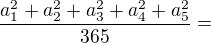


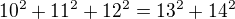
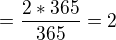
 , potom sa vyraz zjednodusi na
, potom sa vyraz zjednodusi na 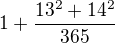 A v duchu nazvu malby dajme tomu, ze
A v duchu nazvu malby dajme tomu, ze 

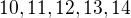 . Skúšal som to isté len pre čísla
. Skúšal som to isté len pre čísla 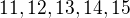 ale tam mi už moc nesedí, lebo
ale tam mi už moc nesedí, lebo  . Ako je možné, že robím nejakú kravinu a Račinského postupnosti som celkom nepochopil.
. Ako je možné, že robím nejakú kravinu a Račinského postupnosti som celkom nepochopil.