Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z diskrétní matematiky
- » Orientace úplného grafu (TOTO TÉMA JE VYŘEŠENÉ)
#1 21. 07. 2010 20:47
Orientace úplného grafu
Zdravím kolegy,
mám tady jednu snad poměrně snadnou úlohu. Je známo, že pro každý orientovaný graf  platí
platí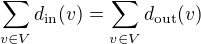 ,
,
kde 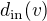 , resp.
, resp. 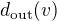 označuje počet orientovaných hran, které do vrcholu
označuje počet orientovaných hran, které do vrcholu  vedou, resp. z něj vedou.
vedou, resp. z něj vedou.
Dokažte, že pokud je  nějakou orientací úplného grafu, pak platí také
nějakou orientací úplného grafu, pak platí také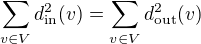
(orientací "běžného" grafu rozumíme orientovaný graf, který z tohoto grafu vznikne nahrazením každé neorientované hrany právě jednou orientovanou hranou o libovolné orientaci).
Offline
- (téma jako vyřešené označil(a) Olin)
#2 21. 07. 2010 22:37
- check_drummer

- Příspěvky: 5451
- Reputace: 106
Re: Orientace úplného grafu
Postupoval jsem takto:
"Máte úhel beta." "No to nemám."
Offline
#3 23. 07. 2010 11:03 — Editoval petrkovar (23. 07. 2010 11:06)
Re: Orientace úplného grafu
Můžeme postupovat i přímo.
Protože 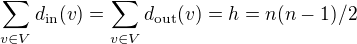 (
( je počet hran) a protože v kompletním grafu je
je počet hran) a protože v kompletním grafu je 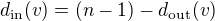 , tak úpravou
, tak úpravou 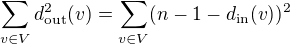 dostaneme
dostaneme 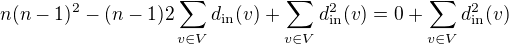 .
.
V úpravě jsme nevyužili, že graf je kompletní, ale jen že je pravidelný.
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z diskrétní matematiky
- » Orientace úplného grafu (TOTO TÉMA JE VYŘEŠENÉ)
