Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Fyzika
- » Soustavy spojene vlaknem (priklad z Feynmana) (TOTO TÉMA JE VYŘEŠENÉ)
#1 11. 08. 2010 18:50
Soustavy spojene vlaknem (priklad z Feynmana)
Ahoj, resim jeden priklad a za boha nemuzu prijit na to co delam spatne. . .
Civka je slozena ze dvou stejnych kotoucku s polomerem  a hmotnosti
a hmotnosti  nasazenych na lehke osicce s polomerem
nasazenych na lehke osicce s polomerem  . Nit navinuta na ose civky je pripevnena ke stropu. Vzdalenost civky od stropu je
. Nit navinuta na ose civky je pripevnena ke stropu. Vzdalenost civky od stropu je  . Z teto polohy se civka zacne spoustet dolu.
. Z teto polohy se civka zacne spoustet dolu.
Jake je svisle zrychleni teziste civky?
(nevim jestli je z popisu jasna situace - kdyby ne, tak nakreslim obrazek, ale pri mem umeni v metapostu to bude na dyl . . . ). Jestli nekdo mate Feynmana 1 tak je to str 272 priklad 19.17. .
Moje reseni:
pohybova rovnice soustavy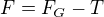 , kde
, kde  je vysledna sila urcyhlujici teziste soustavy,
je vysledna sila urcyhlujici teziste soustavy,  je gravitacni sila,
je gravitacni sila,  je tazna sila lana
je tazna sila lana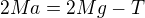 (dosazeny hodnoty ze zadani)
(dosazeny hodnoty ze zadani)
tazna sila  roztaci soustavu civek, tedy plati
roztaci soustavu civek, tedy plati 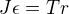
pro moment setrvacnosti soustavy plati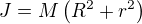 (
( se krati s
se krati s  kvuli poctu civek. . )
kvuli poctu civek. . )
a pro uhlove zrychleni plati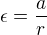
Po dosazeni a vyjadreni mi vyslo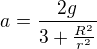
a spravny vysledek dle knihy je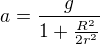
Fakt nevim co mam spatne. . . . Za jakoukoli radu Diky moc.
pi = 3
Offline
- (téma jako vyřešené označil(a) Azeret)
#2 11. 08. 2010 19:55 — Editoval jelena (11. 08. 2010 19:56)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Soustavy spojene vlaknem (priklad z Feynmana)
↑ Azeret:
Zdravím,
když se dívám na zadání z ruského vydání Sbírky příkladů (1967), číslování stejné (str. 62 djvu) - tak je přímo uvedeno, že hmotnost civky je zanedbatelná, tedy v momentu setrvačnosti (myslím) nemá byt malé r, ale jen 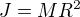 (1/2 se kratí jak píšeš).
(1/2 se kratí jak píšeš).
Pomůže?
Řešení jsou od str. 114 djvu (pokud budeš potřebovat nějaký krátký pracovní překlad, děj vědět).
Offline
#3 11. 08. 2010 20:41 — Editoval Azeret (11. 08. 2010 21:10)
Re: Soustavy spojene vlaknem (priklad z Feynmana)
↑ jelena:
Tak jsem to spocitala pomoci tve aproximace a vysel spravny vysledem, ale teda nechapu proc se takove aproximace dela. . . vzdyt to jde bez problemu spocitat i bez ni.
Navic mi prijde trochu nelogicka ( pokud je mala civka nehmotna, tak se jedna o duty valec a ten ma moment setrvacnosti 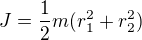 . . . . na vztah, ktery pises (a ktery je dle vysledku spravny) by se to podle me redukovalo k
. . . . na vztah, ktery pises (a ktery je dle vysledku spravny) by se to podle me redukovalo k
kdyby byla zanedbatelna hmotnost male civky a take jeji polomer (ale to by tam pak nebyl zadny rotacni moment . .). ). . . . .No ta aproximace se mi proste fyzikalne nelibi. .
ale co uz -diky moc (jinak bych to pocitala dalsich spoustu dni :) )
pi = 3
Offline
#4 11. 08. 2010 21:35
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Soustavy spojene vlaknem (priklad z Feynmana)
↑ Azeret:
Také děkuji a také si myslím, že to překombinovali - když je v zadání "kotouč", tak si představim, že je plný. Ale, jak píšeš, bez civky by nešlo přenášet rotaci.
Offline
Stránky: 1
- Hlavní strana
- » Fyzika
- » Soustavy spojene vlaknem (priklad z Feynmana) (TOTO TÉMA JE VYŘEŠENÉ)