Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 14. 08. 2010 19:31
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Riemannova hypotéza
A jak to počítáš? Pokud jako sumu ,
,
tak ta podle wikipedie konverguje pouze pro komplexní  , jejichž reálná část je větší než jedna. Do
, jejichž reálná část je větší než jedna. Do 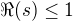 se funkce musí analyticky rozšířit.
se funkce musí analyticky rozšířit.
Offline
#3 14. 08. 2010 19:39
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Riemannova hypotéza
Zde a po kliknutí na "Next: Zeta záporných sudých" je nejspíš (je to delší doba, co jsem to četl) to, hledáš.
Offline
#7 15. 08. 2010 18:22
- check_drummer

- Příspěvky: 4900
- Reputace: 105
Re: Riemannova hypotéza
Existuje nějaký materiál (článek) popisující, jakým způsobem lze analyticky rozšířit danou funkci (např. právě tu Riemannovu)? Zda je toto rozšíření jednoznačné (nespíš je, pokud budeme mít na rozšíření nějaké vhodné požadavky), atd. Díky.
"Máte úhel beta." "No to nemám."
Offline