Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 12. 08. 2010 20:37 — Editoval jelena (12. 08. 2010 20:48)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Limita
↑ Maggie:
vyznáš se v takových úpravách? http://forum.matweb.cz/viewtopic.php?pid=27971#p27971
měla bys dostat takový zápis: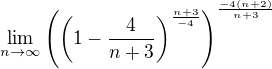
Případně se ozví. Ať se to podaří.
Offline
#4 13. 08. 2010 09:29
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Limita
A pokud by se ti nelíbily jednoduché metody a toužilas po něčem složitějším, tak lze postupovat i takto: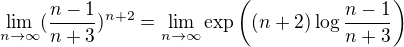
Pak pomocí nějaké věty o limitě složené funkce budu počítat jen limitu exponentu, kde ale použiješ známou tabulkovou limitu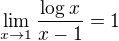 a vhodným rozšířením ji tam vsuneš.
a vhodným rozšířením ji tam vsuneš.
Samozřejmě to celé okomentuješ a vysvětlíš, proč můžeš použít limitu funkce u limity posloupnosti apod.
Offline
#5 14. 08. 2010 14:54
Re: Limita
Děkuji vám všem za rady, mám ještě jiný postup, pomocí substituce, tak bych vás požádala o kontrolu, jestli to takto lze řešit. Výsledek mi to dalo správný ve dvou podobných příkladech a zřejmě je to něco podobného, ne-li stejného, jako psal Rumburak, ale zdá se mi to asi nejrychlejší a nejjednodušší řešení.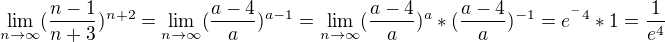
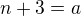
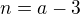
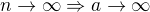
Offline
#6 15. 08. 2010 09:36
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Limita
↑ Maggie:
Zdravím,
uvědomuji si, že nereagování na ténto dotaz by mohlo brzdit v postupu v další přípravě, tak mé vyjádření:
1) neopodstatněné substituce nemám příliš v oblibě, ale pokud tato substituce pomáhá uvědomit (nebo dojit k závěru), že 3=-1+4 a 2=3-1, tak určitě subsituci zaved.
Bude fungovat i na zadání typu 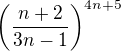 , ale to věc estetického pohledu.
, ale to věc estetického pohledu.
2) po substituci oprav, prosím, po "=" místo 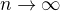 už má být
už má být 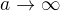 ,
,
3) po třetím "=" bych ještě doplnila mezikrok, ve kterém by bylo vidět, že se podařilo dojit na úpravu "2. pozorůhodné limity" (na důsledek 1) a že máme součin limit (ještě v druhé závorce provest vytknutí a).
4) není možné začit věřit metodě jen proto, že "Výsledek mi to dalo správný ve dvou podobných příkladech..." (c),
5) ano, je to velmi podobné na postup od váženého kolegy Rumburaka.
Doufám, že jsem přípravě na zkoušky neubližila. Případně se mi dostane řádného pokárání od vážených kolegů, děkuji.
OT: ↑ halogan:
Offline
#7 15. 08. 2010 11:33
Re: Limita
↑ jelena:
Děkuji ještě jednou za reakci i připomínky. Abych pravdu řekla, jsem ráda, když to "nějak" vypočítám, ale je mi jasné, že tenhle přístup zde nebude moc ceněn. Prostě potřebuju ty zákonitosti vidět nějak polopaticky, aby mi to seplo, proto pro mě některé úpravy nejsou moc schůdné, někdo to tam vidí hned, já si to musím několikrát přepsat...
Že mi to vyšlo na dvou příkladech jsem dala pouze k dobru, nevycucala jsem si to jen tak z prstu, měla to takhle v poznámkách kolegyně z doučování od našeho profesora. Jak už jsem si párkrát ověřila, učí matematiku trochu jinak, má trochu jiné požadavky a metody než třeba na velmi podobných fakultách jiní učitelé. Což není žádná výmluva, jen prostě je to pro mě někdy hůř stravitelné a proto hledám rady i jinde.
Rusky neumím, důsledek 1 jsem tam ani po přeložení stránky nenašla, ale pokusila jsem se to upravit dle tvých instrukcí, má to být takhle? 
Každopádně moc děkuji a abych vám dodala naději, že už nebudu dlouho otravovat, tak zkoušku mám 20.8. :o)
Offline
#8 15. 08. 2010 12:36
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Limita
↑ Maggie:
také děkuji. Tvému přístupu není vůbec co vytknout - problémy jasně formuluješ, píšeš své návrhy. Neotravuješ vůběc a moc přeji, aby příprava na zkoušku byla efektivní a zkouška byla úspěšná.
Odkaz na ruskou stranku dávám proto, že jsem nenašla jinou, kde jsou obě pozoruhodné limity, včetně důsledků a důkazů (po rozklíknutí), omlouvám se, že nemám lepší jazykovou variantu, snad někdo z kolegů.
Už jen tato úprava tohoto "kousku" mi ve Tvém zápisu chybí: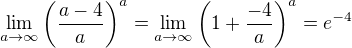 viz i doporučení o "využití znamého vzorce" (to je 1. důsledek) od ↑ Rumburak:
viz i doporučení o "využití znamého vzorce" (to je 1. důsledek) od ↑ Rumburak:
Maggie napsal(a):
tenhle přístup zde...
spíš si uvědomuji, jak moc sem "zde" já nepatřím (moje názory snad nejsou až tak překvapivé - konec konců jsi již měla možnost seznamit, když jsem se pohoršovala nad úlohou o dcerách a matkách běhajících po lesích).
Pokud v mém výkladu je nějaká nepřesnost, děkuji kolegům (co sem patří) o upozornění a o nápravu.
Offline
#9 15. 08. 2010 12:55
Re: Limita
↑ jelena:
Jasně, pro úplnost by tam tenhle krok neměl chybět, i když tam už je to i pro mě zřejmé, že se jedná o totéž.
Jo, to byly ty příklady k přijímačkám, ty byly fakt zábavné :o) To taky vymýšlel pan profesor...
Označuji za vyřešené a ještě jednou děkuji vám všem, jste velká pomoc, když už fakt nevím, kudy kam.
Offline
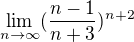
 .
.