Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 03. 04. 2008 17:52
- Honza Bohuslav
- Zelenáč
- Příspěvky: 19
- Reputace: 0
Povrch krychle
Povrchy dvou krychlí, z nichž jedna má hranu o 22 cm delší než druhá, se od sebe liší o 19272 cm2. Vypočítejte délku hran obou krychlí.
Offline
#2 03. 04. 2008 18:52 — Editoval Marian (03. 04. 2008 19:00)
Re: Povrch krychle
Pokud a bude delka hrany puvodni krychle a b bude delka hrany zvetsene krychle (b=a+22 [cm]), pak pro jejich povrchy P_1 a P_2 plati
Pro rozdil techto krychli plati vztah (ze zadani) P_2-P_1=19272 [cm^2]. To clekem dava jiz dva vztahy pro nezname a a b:
Pokud prvni zaramovanou rovnici podelis sestkou a u druhe prevedes a-cko na levou stranu, mas soustavu dvou (nelinearnich) rovnic:
Protoze je ale 
davaji soustava rovnic vyse vztah
Dohromady s faktem, ze b-a=22, mas sectenim s rovnici b+a=146 vysledek 2b=168, odkud b=84. Odectenim 22 od cisla b pak dostanes take cislo a, ktere reprezentuje delku hrany puvodni krychle.
*** pracuji ***
Offline

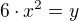
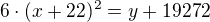
 a zbude
a zbude  , tedy
, tedy