Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z algebry
- » Výraz probíhající (téměř) všechna prvočísla (TOTO TÉMA JE VYŘEŠENÉ)
#1 19. 08. 2010 22:22
- check_drummer

- Příspěvky: 4952
- Reputace: 106
Výraz probíhající (téměř) všechna prvočísla
Dokažte, že množina 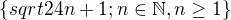 obsahuje všechna prvočísla větší než 3.
obsahuje všechna prvočísla větší než 3.
"Máte úhel beta." "No to nemám."
Offline
- (téma jako vyřešené označil(a) halogan)
#2 19. 08. 2010 23:12
#3 21. 08. 2010 21:39
- check_drummer

- Příspěvky: 4952
- Reputace: 106
Re: Výraz probíhající (téměř) všechna prvočísla
↑ halogan:
Je to tak. Možná by šlo pro ověření, že 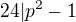 postupovat i tak, že:
postupovat i tak, že:
1) z 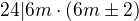 plyne, že
plyne, že 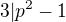
2) z toho, že p-1 a p+1 jsou dvě po sobě následující sudá čísla a tedy je jedno z nich dělitelné 4 a tedy je jejich součin dělitelný 8, plyne, že 
"Máte úhel beta." "No to nemám."
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z algebry
- » Výraz probíhající (téměř) všechna prvočísla (TOTO TÉMA JE VYŘEŠENÉ)

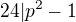 , kde
, kde  je libovolné prvočíslo větší než 3.
je libovolné prvočíslo větší než 3.
 (pro každé prvočíslo větší než 3 najdu celé číslo
(pro každé prvočíslo větší než 3 najdu celé číslo  takové, že buď 6m - 1 = p, nebo 6m + 1 = p) — toto je jasné, nebo to musím též dokázat?
takové, že buď 6m - 1 = p, nebo 6m + 1 = p) — toto je jasné, nebo to musím též dokázat?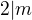 a
a 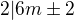 . Hotovo.
. Hotovo. . Jelikož ale
. Jelikož ale 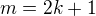 (pro
(pro 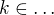 ), tak řeším
), tak řeším  , což očividně platí.
, což očividně platí.