Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 21. 08. 2010 15:53
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
analytická geometrie 2.
Ahoj, strašně moc prosím o pomoc. Narazila jsem na pár úkolů a vůbec si s něma nevím rady. Děkuji za rady a nakopnutí.
1) Vypočtěte délky výšek v trojúhelníku ABC, je-li A=[3,7], B=[5,-1], C=[-3,5].
2)Určete velikost stran a vnitřních úhlů trojúhelníku ABC, je-li A=[7,-3], B=[1,8], C=[-4,3]
Offline
- (téma jako vyřešené označil(a) Lucinecka88)
#2 21. 08. 2010 16:55
- teolog


- Místo: Praha
- Příspěvky: 3498
- Škola: MFF + PřF UK
- Pozice: Gymnázium Přírodní škola - učitel (M, Z)
- Reputace: 167
Re: analytická geometrie 2.
↑ Lucinecka88:
K příkladu 1):
Na výpočet délky výšky potřebujeme znát dva koncové body. Jedním bodem je vrchol, který známe ze zadání. Druhý bod je průsečík výšky a strany na výšku kolmé.
Pro výpočet průsečíku je nutné znát rovnice obou přímek (výšky a strany).
Rovnici strany dát dohromady ze zadaných bodů už umíte (viz Váš postup).
Rovnici výšky umíte rovněž (viz tento postup).
Takže pomocí již naučeného získáte dvě rovnice. Z nich spočítáte průsečík.
A pak už stačí jen použít vzorec na vzdálenost dvou bodů.
Offline
#3 21. 08. 2010 16:58
- teolog


- Místo: Praha
- Příspěvky: 3498
- Škola: MFF + PřF UK
- Pozice: Gymnázium Přírodní škola - učitel (M, Z)
- Reputace: 167
Re: analytická geometrie 2.
↑ Lucinecka88:
K příkladu 2):
Ze vzorce pro vzdálenost bodů snadno spočítáte délky stran.
Pro velikost vnitřních úhlů lze použít vzorec pro odchylku vektorů. Takže pro každou stranu je nutné najít směrový vektor a pro každou dvojici stran pomocí dvojice vektorů se úhel spočítá poměrně snadno.
Offline
#4 22. 08. 2010 12:06
#5 22. 08. 2010 14:03
Offline
#6 22. 08. 2010 14:12
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: analytická geometrie 2.
↑ jarrro:
Nechápu jak to myslíš. Děkuji za vysvětlení.
Offline
#9 22. 08. 2010 14:41
Re: analytická geometrie 2.
↑ Lucinecka88:nekontroloval som to len som odpovedal na otázku akú rovnicu použiť na zistenie vzdialenosti dvoch bodov je to z pytagorovej vety odmocnina zo súčtu mocnín rozdielov súradníc a Mr.Pinker má pravdu pri výškach stací skúmať vzdialenosť protiľahlej strany od vrcholu
MATH IS THE BEST!!!
Offline
#10 22. 08. 2010 17:49
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: analytická geometrie 2.
Děkuji všem, ale ted jsem trochu v prdeli s tím jak to mám vypočítat.
Offline
#12 23. 08. 2010 07:43 — Editoval Cheop (23. 08. 2010 08:08)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: analytická geometrie 2.
↑ Lucinecka88:
Výška na stranu a (v_a)
Směrový vektor přímky BC 
Normálový vektor je (3; 4)
Rovnice přímky BC je: dosazení bodu B dopočteme c
dosazení bodu B dopočteme c
3*5-4+c=0
c=-11
Rovnice přímky BC je:
Velikost výšky v_a je vzdálenost bodu A od přímky BC
Obecně:
Máme-li přímku  a bod A (x_0; y_0) pak vzdálenost je:
a bod A (x_0; y_0) pak vzdálenost je: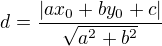 tedy:
tedy:
Obdobně vypočítáš délky ostatních 2 výšek
Obrázek
Nikdo není dokonalý
Offline
#13 23. 08. 2010 08:37
- teolog


- Místo: Praha
- Příspěvky: 3498
- Škola: MFF + PřF UK
- Pozice: Gymnázium Přírodní škola - učitel (M, Z)
- Reputace: 167
Re: analytická geometrie 2.
↑ Lucinecka88:
Jestli jsem Vás nějak svým návrhem postupu zmátl, tak se omlouvám. Je pravda, že postup od kolegů je rychlejší a jednodušší.
Mne jen při tom zadání napadlo využít toho, co jsme spolu počítali den před tím. Proto jsem ten postup volil jako průsečík dvou přímek.
Offline
#14 23. 08. 2010 09:53 — Editoval Cheop (23. 08. 2010 13:36)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: analytická geometrie 2.
↑ Lucinecka88:
2)
Vzdálenost AB
Vzdálenost AC
Vzdálenost BC
Výpočet úhlu alfa


Ostatní 2 úhly stejným způsobem.
Nebo si všimnout, že trojúhelník je rovnoramenný, a proto úhly beta a gama mají stejnou velikost.
tedy:
Nikdo není dokonalý
Offline
#15 23. 08. 2010 11:23 — Editoval Lucinecka88 (23. 08. 2010 11:33)
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: analytická geometrie 2.
Děkuji všem za pomoc. omlouvám se že jsem tu dřív nenapsala,ale dneska jsem měla zkoušku z ekonomiky tak jsem se učila na to. Strašně moc děkuji za vysvětlení té 1 kratším způsobem. Ještě bych se chtěla zeptat, nemá se u 1 do té rovnice dosadit bod A, aby jsme zjistili to c?
Offline
#16 23. 08. 2010 11:36 — Editoval Cheop (23. 08. 2010 11:37)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: analytická geometrie 2.
↑ Lucinecka88:
Ne, pro zjištění c musíš dosadit bod B nebo C, protože strana a (BC) prochází uvedenými body.
Výška je kolmá na tuto stranu a a ta prochází bodem A.
Velikost tévýšky vypočítáš jako vzdálenost bodu A od přímky BC
dle výše uvedeného vzorce.
Nikdo není dokonalý
Offline
#17 23. 08. 2010 11:37
Re: analytická geometrie 2.
↑ Lucinecka88:ak myslíš priamku BC tak bod A na nej neleží
MATH IS THE BEST!!!
Offline
#18 23. 08. 2010 11:40
#19 23. 08. 2010 12:14
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: analytická geometrie 2.
Mám tu 1 prosím správně vypočítané?
a=5,2
b=8,2
c=6,3
Offline
#20 23. 08. 2010 12:39
#21 23. 08. 2010 14:18
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: analytická geometrie 2.
Děkuji všem za velkou pomoc.
Offline

![kopírovat do textarea $A=\left[x_1;y_1\right],B=\left[x_2;y_2\right]$](/mathtex/89/897274fee159bf9436fd752cd163efde.gif) potom
potom

 ale
ale 

