Matematické Fórum

faktorial

Znenie ulohy:
Vypocitajte dlzky stran trojuholnika ABC, ak su v pomere 4:13:15 a obsah je 216cm2.

ja som to vypocital na 8,6,30 su strany, lenze ten moj postup nie je spravny, no mozno je ale ucitelka by mi ho neuznala. mohol by niiekto skontrolovat a popripade napisat jeho postup?

dakujem

Tychi · 05. 09. 2010 17:18

já se dopočítala k číslům 12, 39, 45

a jak?
strany lze z toho poměru vyjádřit jako
$a=4x$ , $b=13x$ , $c=15x$

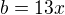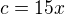
Najdi si vzorec pro výpočet obsahu trojúhelníka, když znáš tři strany. Do něj dosaď S, a, b, c a vypočti x.
Pak se vrať k vyjádření stran a máš hotovo.

faktorial · 06. 09. 2010 13:08

lenze ja nepoznam vzorec na vypocet obsahu trojuholnika pomocou vsetkych stran iba:
S=(a*va)2
alebo S=(a*b)/2 pre pravouhly trojuholnik ked c je odvesna

Cheop · 06. 09. 2010 13:22 — Editoval Cheop (06. 09. 2010 14:27)

↑ faktorial:
Použij Heronův vzorec.
$S=\sqrt{s(s-a)(s-b)(s-c)}$ kde $s=\frac{a+b+c}{2}$ a, b, c jsou strany trojúhelníka
Naše strany budou: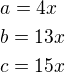
$a=4x\nlb=13x\nlc=15x$
$s=\frac{4x+13x+15x}{2}=16x\nls-a=16x-4x=12x\nls-b=16x-13x=3x\nls-c=16x-15x=x$
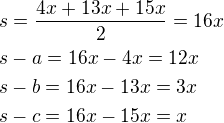
Dosadíme do Heronova vzorce a dostaneme: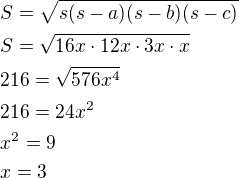
$S=\sqrt{s(s-a)(s-b)(s-c)}\nlS=\sqrt{16x\cdot 12x\cdot 3x\cdot x}\nl216=\sqrt{576x^4}\nl216=24x^2\nlx^2=9\nlx=3$
$a=4x\nla=4\cdot 3=12\nlb=13x\nlb=3\cdot 13=39\nlc=15x\nlc=15\cdot 3=45$
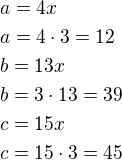
Strany trojúhelníka, které jsou v poměru 4:13:15 o obsahu 216 jsou: 12, 39, 45

faktorial

no tak dakujem za riesenie. chcem sa spytat ci neexistuje aj nejake ine riesenie nakolko my sme sa Heronov vzorec neucili. Ale inac pekne jednoduche riesenie.

dakujem

Cheop · 06. 09. 2010 13:42 — Editoval Cheop (06. 09. 2010 16:58)

↑ faktorial:
Šlo by to počítat pomocí kosinové věty a pak pro obsah použít: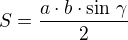
$S=\frac{a\cdot b\cdot\sin\,\gamma}{2}$
Kosinová věta: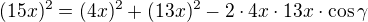
$(15x)^2=(4x)^2+(13x)^2-2\cdot 4x\cdot 13x\cdot\cos\gamma$ - úpravou: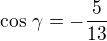
$\cos\,\gamma=-\frac{5}{13}$
$\sin\,\gamma=\sqrt{1-\cos^2\gamma}\nl\sin\,\gamma=\sqrt{1-\frac{25}{169}}\nl\sin\,\gamma=\frac{12}{13}$
$S=\frac{4x\cdot 13x\cdot\sin\,\gamma}{2}\nl216=\frac{52x^2\cdot 12}{2\cdot 13}\nl24x^2=216\nlx^2=9\nlx=3$

$a=4x\nla=4\cdot 3=12\nlb=13x\nlb=3\cdot 13=39\nlc=15x\nlc=15\cdot 3=45$

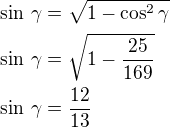
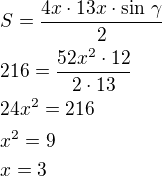
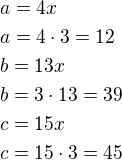
PS: Překvapivě je výsledek stejný jako v příspěvku #4