Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 12. 09. 2010 23:52
Vedenie tepla
Zdravím,
popri štúdiu ODR a PDR som sa (ako nefyzik) dostal k dvom modelom. Prvý je model ODR, s ktorým som sa stretol už na strednej škole v zbierke úloh a opisuje ochadzovanie (zohrievanie) telesa podľa teploty prostredia![kopírovat do textarea $\frac{\rm{d}T(t)}{\rm{d}t}=\alpha\cdot[T_p-T(t)]$](/mathtex/aa/aa4aeccc34955e39b365f10eb9d9740c.gif)
kde 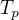 je teplota prostredia. Riešenie je
je teplota prostredia. Riešenie je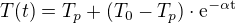
Pri PDR som sa stretol so známou Heat equation. Otázka smeruje tam, čo majú tieto dve rovnice spoločné. Ide o dva modely, pričom popisujú v podstate podobný jav. Podľa mňa, funkcia T, ktorá spĺňa PDR vedenia tepla, pri zafixovaní priestorových súradníc by mala spĺňať aj spomenutú ODR.
Ďakujem za objasnenie :-)
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
- (téma jako vyřešené označil(a) lukaszh)
#2 15. 09. 2010 05:17 — Editoval medvidek (15. 09. 2010 05:27)
Re: Vedenie tepla
... funkcia T, ktorá spĺňa PDR vedenia tepla, pri zafixovaní priestorových súradníc by mala spĺňať aj spomenutú ODR.
Myslím, že toto tvrdenie obecne neplatí. Ako protipríklad urobme nasledujúci myšlienkový experiment:
Majme tepelne izolujúce prostredie, v ktorom sa nachádzajú dve vzájomne oddelené telesá z rovnakého (tepelne vodivého) materiálu o hmotnostiach 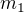 ,
, 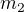 a teplotách
a teplotách  ,
, 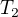 . Predpokladajme, že
. Predpokladajme, že  a zároveň
a zároveň  . V čase
. V čase  tieto telesá k sebe priložíme a budeme sledovať zmeny teploty v okolí styčnej plochy (predpokladáme, že tvar telies je taký, aby styčná plocha bola nenulová, inak by ku žiadnemu vedeniu tepla nedochádzalo).
tieto telesá k sebe priložíme a budeme sledovať zmeny teploty v okolí styčnej plochy (predpokladáme, že tvar telies je taký, aby styčná plocha bola nenulová, inak by ku žiadnemu vedeniu tepla nedochádzalo).
Zamerajme sa napríklad na bod v telese č. 1 (veľkom chladnom), ktorý sa nachádza v tesnej blízkosti styčnej plochy. Teplota v tomto bode najprv stúpne, pretože sa povrch spočiatku ohrieva od telesa č. 2 (malého teplého). Po určitom čase teplota v tomto bode začne klesať a asymptoticky sa približovať k rovnovážnej teplote celého systému. Pokiaľ by bolo  , výsledná rovnovážna teplota by bola blízka pôvodnej teplote
, výsledná rovnovážna teplota by bola blízka pôvodnej teplote  . Takýto priebeh teploty by sme dostali riešením parciálnej dif. rovnice pre vedenie tepla s vhodne zvolenými počiatočnými a okrajovými podmienkami. Je evidentné, že to neodpovedá monotónnemu exponenciálnemu priebehu, ktorý je riešením ODR z príspevku #1.
. Takýto priebeh teploty by sme dostali riešením parciálnej dif. rovnice pre vedenie tepla s vhodne zvolenými počiatočnými a okrajovými podmienkami. Je evidentné, že to neodpovedá monotónnemu exponenciálnemu priebehu, ktorý je riešením ODR z príspevku #1.
Model s ODR je niečo trochu iné, môžeme ho chápať ako integrálny popis skutočnosti. Avšak podľa môjho názoru, aby sa táto rovnica dala považovať za presnú, mali by sme ju zapisovať napríklad takto
Na ľavej strane je časová zmena energie v danom uzavrenom objeme, na pravej strane je integrál cez plochu uzatvárajúcu tento objem. V tejto rovnici  predstavuje koeficient prestupu tepla na rozhraní určenom plochou
predstavuje koeficient prestupu tepla na rozhraní určenom plochou  .
.
Skôr sa teda jedná o integrálny vzťah pre prestup tepla než o model vedenia tepla.
Offline
#3 15. 09. 2010 10:35
Re: Vedenie tepla
↑ medvidek:
Výborne, ďakujem.
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#4 15. 09. 2010 16:12
Re: Vedenie tepla
↑ lukaszh:
Dovolil bych si přihodit ještě jeden postřeh. A tím je jakási geometrická představa Laplaceova operátoru (v kart. souřadnicích součet druhých parciálních derivací). Jedná se v podstatě o rozdíl hodnoty dané veličiny v konkrétním bodě od hodnoty aritmetického průměru z okolních blízkých bodů. V této představě se pak uvažuje limitně malá oblast. Takto se dá představit Laplace. A ta ODR vlastně říká že teplota se někde mění, pokud je v kontaktu s tělesem o jiné teplotě. Tedy na tu PDR rovnici vedení tepla (RVT) můžeme nahlížet tak, že daný bod odevzdává teplo všem okolním bodům, co jsou chladnější (a intenzita tohoto přenosu závisí lineárně na rozdílu teplot) a zároveň příjmá teplo od všech co jsou teplejší. Po vzájemné kompenzaci tedy lze říci, že daný bod odevzdává/příjmá teplo podle toho, jaká je střední hodnota rozdílu teplot od okolních bodů a tím se dostáváme ke geometrické interpretaci Laplaceova operátoru. Ten vztah pro ODR je dost obecný a v podstatě je to přímý důsledek jedné z definic teploty (teplo se přenáší z tělesa o větší teplotě na těleso s menší a přenos teplené energie je lineárně úměrný rozdílu teplot). RVT je pak důsledek tohoto principu.
Samozřejmě, že se to celé dá vykládat tak, že se postuluje platnost RVT a od ní se odvodí všechny ostatní rovnice o teple. Je to zřejmě lépe matematicky pochopitelný krok, ale není už tolik intuitivní - nevidíme v něm, proč vlastně RVT platí.
1 + 1 = 1 + 1
... a nebo taky ne
Offline
#5 15. 09. 2010 18:39
Re: Vedenie tepla
↑ rughar:
Vďaka, ale dá sa tá predstava L-operátora nejako podložiť? Keď vezmem limitne malú oblasť tak rozdiely teplôt predsa konvergujú k nule (za predpokladu hladkej funkcie). Inak super ...
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#6 15. 09. 2010 19:30 — Editoval rughar (15. 09. 2010 19:34)
Re: Vedenie tepla
↑ lukaszh:
Ono to teda není čistě rozdíl. Ale rozdíl v závislosti na dráze. Podobně jako derivace není vlastně rozdíl funke ve dvou blízkých bodech ale rozdíl ve dvou blízkých bodech v poměru k jejich vzdálenosti, tak podobně u Laplase (pro funkci dvuo proměnných) je to![kopírovat do textarea $\rm{\Delta} f(x,y) = 4\lim_{h\rightarrow 0} \frac{[f(x + h,y) + f(x-h,y)+f(x ,y+h)+f(x,y-h)]/4-f(x ,y)}{h^2} $](/mathtex/bb/bb568f6ec32c1960aeca4b81be463539.gif)
To že jsem napsal, že Laplace "je" roven rozdílu od aritmetického průměru okolí nebylo myšleno doslova. Ale je to tomu úměrné. Fakt, že výše uvedená limita odpovídá též součtu druhých parciálních derivací podle jednotlivých proměnných x a y si může každý odvodit už sám, pokud by jej to zajímalo. A ona geometrická interpretace, o které jsem mluvil, je tam zjevně patrná z čitatele toho zlomku.
1 + 1 = 1 + 1
... a nebo taky ne
Offline
