Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 20. 09. 2010 16:22 — Editoval DanG (20. 09. 2010 16:43)
Rovnice s parametrem
Pěkný den, pomohli byste mi, prosím vás, vyřešit dvě rovnice s parametrem? Už si s tím lámu hlavu docela dlouho, ale pořád se něják nemohu dostat ke správnému řešení a diskusi. Ty zapeklité rovnice jsou následující:
a) 
b) 
(Neznámá je X a parametr je A, které patří do R)
Děkuji :)
Offline
- (téma jako vyřešené označil(a) jelena)
#2 20. 09. 2010 16:48 — Editoval b.r.o.z1 (20. 09. 2010 17:00)
Re: Rovnice s parametrem
ok jdu na to:-)
takže a)
1) 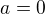 =>lineární rovnice
=>lineární rovnice  =>
=> 
2) 


a) D > 0 => 2 reálné kořeny
b) D=0 => a=0 ale toto nastat nemůže viz. nahoře jsme to zakázali
c) D<0 toto řešení lze jen v C(komplexní čísla), neboť zápornou odmocninu v reálných číslech neznáme.
Závěr:
1) Je-li a=0, pak K={} (prázdná množina).
2) Je-li  , pak
, pak 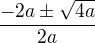
imho je to vše
"Vím, že nic nevím." Sokrates
Offline
#3 20. 09. 2010 16:51 — Editoval teolog (20. 09. 2010 16:52)
- teolog


- Místo: Praha
- Příspěvky: 3497
- Škola: MFF + PřF UK
- Pozice: Gymnázium Přírodní škola - učitel (M, Z)
- Reputace: 167
Re: Rovnice s parametrem
↑ DanG:
Pěkný den rovněž,
ukáži postup pro ten druhý. První je podobný.
Cílem je rovnici upravit do tvaru x=...

 za předpokladu, že
za předpokladu, že  , tedy
, tedy  a
a 



Pro 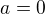 je
je 
Pro 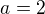 je
je 
Pro  je
je 
Offline
#4 20. 09. 2010 16:59
- teolog


- Místo: Praha
- Příspěvky: 3497
- Škola: MFF + PřF UK
- Pozice: Gymnázium Přírodní škola - učitel (M, Z)
- Reputace: 167
Re: Rovnice s parametrem
↑ b.r.o.z1:
...nevím jak se v Texu zapisuje prázdná množina
Také jsem nad tím dumal. Je to \empty
Offline