Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 22. 09. 2010 14:30 — Editoval Cheop (23. 09. 2010 11:37)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Zkouška u lichobežníku.
Nikdo není dokonalý
Offline
#5 22. 09. 2010 15:31 — Editoval teolog (22. 09. 2010 15:34)
- teolog


- Místo: Praha
- Příspěvky: 3497
- Škola: MFF + PřF UK
- Pozice: Gymnázium Přírodní škola - učitel (M, Z)
- Reputace: 167
Re: Zkouška u lichobežníku.
↑ Korbulo:
Tomu se neříká zkouška, ale zápis konstrukce.
Není ten postup jasný z Cheopova obrázku?
Offline
#7 22. 09. 2010 15:57 — Editoval b.r.o.z1 (22. 09. 2010 15:59)
Re: Zkouška u lichobežníku.
↑ Korbulo:
1) AB, |AB|=6cm
2) p, p||AB, |p,AB|=3cm
3) k, k(B, 4cm)
4)C, C 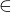 p
p 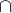 k
k
5)l, l(C, 2 cm)
6) D, D 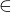 p
p 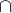 l
l
7) lich. ABCD
třeba takhle
Cheope prosím, v čem to kreslíš, prosím?:-)
Dík
"Vím, že nic nevím." Sokrates
Offline
#9 22. 09. 2010 16:04
Re: Zkouška u lichobežníku.
↑ Korbulo:
víš je přeci kolmá na stranu c, a zároveň na stranu a, takže výška v_a není nic jiného než vzdálenost strany a a strany c, které jsou rovnoběžné, v mém zápisu to je jako krok číslo 2,
"Vím, že nic nevím." Sokrates
Offline
#11 22. 09. 2010 16:22
- teolog


- Místo: Praha
- Příspěvky: 3497
- Škola: MFF + PřF UK
- Pozice: Gymnázium Přírodní škola - učitel (M, Z)
- Reputace: 167
Re: Zkouška u lichobežníku.
↑ b.r.o.z1:
Já myslím, že to dělá v GeoGebře.
Offline
#14 22. 09. 2010 17:14
Re: Zkouška u lichobežníku.
↑ Korbulo:
na tos přišel jak?
nikde není psáno, že ten lichoběžník je rovnoramenný, ani nemůže být
"Vím, že nic nevím." Sokrates
Offline
#16 22. 09. 2010 17:49 — Editoval b.r.o.z1 (22. 09. 2010 17:53)
Re: Zkouška u lichobežníku.
↑ Korbulo:
nesmysl protože viz. obrázek
Neplatila by Pythagorova věta. Prtže 
Nebo se mýlím mí kolegové?
"Vím, že nic nevím." Sokrates
Offline
#19 22. 09. 2010 18:12 — Editoval Spybot (22. 09. 2010 18:12)
Re: Zkouška u lichobežníku.
↑ Korbulo:
No s udajmi, ktore si poskytol, to nie je mozne. Alebo je v zadani chyba, alebo sa pan ucitel kopol; nevidim ine moznosti.
Offline
#22 22. 09. 2010 18:55 — Editoval Chrpa (23. 09. 2010 11:38)
Re: Zkouška u lichobežníku.
↑ Korbulo:
Aby to byl lichoběžník rovnoramenný pak by musel vypadat takto:
Výška lichoběžníku by musela být
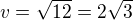
Offline