Matematické Fórum

↑ Deepy:To by mne zajímalo, jakpak se středoškolák dostane k úloze, kterou je možno sformulovat (a vyřešit) pomocí Kirkmanovských systémů trojic. A neúplných k tomu ;-)

Řešení úlohy existuje, nicméně asi nebudu umět podat pěkný popis pro středoškoláka.
Ekistuje tzv. Kirmanovský systém trojic pro 9 prvků. Jeden je např. na druhém řádku od konce na stránce zde.
Použijeme některé (například první) tři sady trojic. Stejné schéma pro zbývajících 9 soutěžících dostaneme přičtením hodnoty 9 (ke každé trojici {i,j,k} přidáme trojici {i+9, j+9, k+9}). Celkem tak dostaneme požadovaný plán pro tři kola.
Poslední nepoužitou sadu trojic {1,6,8}, {2,4,9}, {3,5,7} můžeme použít při konstrukci skupinek pro dalších tři kola.
EDIT:
Je-li například {i,j,k} jedna zatím nevyužitá trojice, tak na stanoviště přidáme tři trojice {i,j,k+9}, {i+9,j,k}, {i,j+9,k} a tři trojice {i+9,j+9,r}, {p,j+9,k+9}, {i+9,q,k+9}, kde je číslo nacházející se na stejné pozici jako hned v následující trojici. Je-li v poslední trojici, vybíráme z první trojice. Podobně je na stejné pozici jako 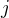a na stejné jako .

Do jakého to je předmětu? Nebo do kroužku? Nebo do programování? Odpověď na tyto otázky mi pomůže při případném dalším popisu řešení.
Nejspíš se očekáválo použití hrubé síly, případně adaptace nějakého postupu probraného v rámci kroužku, že?

↑ Deepy:Aha!
Tabulku sestavím s čísly. Písmena si každý dosadí sám ;-)
{1,2,3}, {4,5,6}, {7,8,9}, {10,11,12}, {13,14,15}, {16,17,18};
{1,4,7}, {2,5,8},{3,6,9}, {10,13,16}, {11,14,17},{12,15,18};
{1,5,9}, {2,6,7}, {3,4,8}, {10,14,18}, {11,15,16}, {12,13,17};

{1, 6, 17}, {2, 4, 18}, {3, 5, 16}, {10, 15, 9}, {11, 13, 7}, {12, 14, 8};
{10, 6, 8}, {11, 4, 9}, {12, 5, 7}, {2, 15, 17}, {3, 13, 18}, {1, 14, 16};
{1, 15, 8}, {2, 13, 9}, {3, 14, 7}, {10, 4, 17}, {11, 5, 18}, {12, 6, 16};

Doufám, že tam nemám chybu.

EIDT: Pokud by stanovišť (a kol) bylo méně stačí nějaký řádek  vynechat.
Pokud by bylo méně hráčů, tak se musí sestavit schéma jinak.
Pro n=15 doporučuji hledat pod heslem "kirkan triple systems".

↑ petrkovar:

Není mi jasné, jak tato tabulka má splňovat požadavek „každý soutěžící musí navštívit jednou každé stanoviště“. Ani prohozením trojic v řádcích toho podle mě není možné dosáhnout. Navíc je každý hráč v jednom kole právě na jednom stanovišti, tedy každý hráč se v každém řádku a sloupci tabulky ↑ Deepy: vyskytuje právě jednou.