Matematické Fórum

Ivana · 27. 09. 2010 17:53

Dobrý den na foru :-)

Tak jsem tu zase s úlohou, kde prosím o pomoc .

V soutěži byly za prvních šest míst vyplaceny odměny v celkové hodnotě 2400 Kč.
Nejvyšší odměna byla za první místo, za další umístění se odměny postupně snižovaly, vždy o stejnou částku.

Platí tvrzení : Součet částek pouze za 1.a 6. místo je roven 800 Kč.

Snažím se příklad dopočítat a stále mi nejdou sestavit rovnice, nebo mi čísla nedávají smysl.

1. rovnice :
$a_1+a_1+(6-1)d=800$
....1. a 6. místo je vyplaceno za 800Kč

2. rovnice :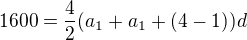
$1600=\frac{4}{2}(a_1+a_1+(4-1))d$
... to je součet vnitřních čtyř členů posloupnosti

A vychází mi nesmyslná čísla :-(

Za pomoc a odpovědi děkuji :-)

Pavel Brožek

Součet prvků aritmetické posloupnosti dostaneš tak, že vezmeš součet prvního (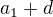 $a_1+d$ ) a posledního ( $a_1+4d$ ) prvku posloupnosti, ten vydělíš dvěma a vynásobíš počtem prvků (4):

$1600=\fra{(a_1+d)+(a_1+4d)}{2}\cdot 4$

Edit: Ale myslím, že se to tady nedá dopočítat. Tvrzení o součtu nejmenší a největší ceny plyne z tvrzení o součtu všech cen. Nemáme dostatek informací k tomu, abychom mohli určit, jaké byly jednotlivé ceny.

Ivana · 27. 09. 2010 18:38

↑ BrozekP: Zdravím :-) a děkuji za odpovědˇ

Tato úloha je z příkladů... novamaturita.cz (rok 2009)
Studenti mají určit platné tvrzení, což je ...

Součet částek pouze za 1.a 6. místo je roven 800 Kč.

Jak tedy mají přijít na to , že toto tvrzení platí ?
Jde o výběr ze čtyř možných odpovědí.
Je možné, že by měli odpovědˇ vybrat intuitivně ?

Pavel Brožek · 27. 09. 2010 18:57

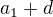Když si označíme částku pro šestého $a_1$ , tak pátý dostane $a_1+d$ a tak dále až první dostane $a_1+5d$ . Je to aritmetická posloupnost, takže její součet bude

$\frac{a_1+(a_1+5d)}{2}\cdot6$

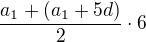
My ze zadání víme, že tento součet je roven 2400.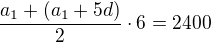

$\frac{a_1+(a_1+5d)}{2}\cdot6=2400$

To upravíme na $2a_1+5d=800$ . A teď se nás ptají na součet ceny prvního a posledního. Tento součet bude

$a_1+(a_1+5d)=2a_1+5d$ .

My ale už víme, čemu je $2a_1+5d$ rovno. Vyšlo nám, že to je rovno 800. Proto s jistotou můžeme ze čtyř nabízených odpovědí

A) Součet částek pouze za 1. a 6. místo je roven 800,– Kč.
B) Součet částek pouze za 1. a 6. místo je roven 1 200,– Kč.
C) Součet částek pouze za 1. a 6. místo je větší než 1 200,– Kč.
D) Součet částek pouze za 1. a 6. místo nelze jednoznačně určit.

vybrat odpověď A).

Ivana · 27. 09. 2010 19:07

↑ BrozekP: Ano , děkuji ,tak to bude :-)

nareklam · 27. 09. 2010 19:25

Přesně toto jsem řešil včera zde. :)

Ivana · 27. 09. 2010 19:27

↑ nareklam: :-)
Ano je to tak , nestíhám hledat v tématech...
Zdravím a přeji hodně úspěchů při řešení :-)

Pavel Brožek · 27. 09. 2010 19:28

↑ nareklam:

Díky za odkaz. Vidím, že jsem to zbytečně moc rozepisoval, neuvědomil jsem si, že se hledaný součet prvního a posledního členu vyskytuje přímo ve vzorci. :-)

Matematické Fórum

#1 27. 09. 2010 17:53

Úloha na posloupnost

#2 27. 09. 2010 17:58 — Editoval BrozekP (27. 09. 2010 18:02)

Re: Úloha na posloupnost

#3 27. 09. 2010 18:38

Re: Úloha na posloupnost

#4 27. 09. 2010 18:57

Re: Úloha na posloupnost

#5 27. 09. 2010 19:07

Re: Úloha na posloupnost

#6 27. 09. 2010 19:25

Re: Úloha na posloupnost

#7 27. 09. 2010 19:27

Re: Úloha na posloupnost

#8 27. 09. 2010 19:28

Re: Úloha na posloupnost

Zápatí