Matematické Fórum

martin2z

Ahoj, potřeboval bych poradit s tímto příkladem z diskriminantu, jedná se o část pod
diskriminantem a znaménka (ve spojitosti i před tím diskriminantem, odmocnina je označená sqrt, x_12 jsou kořeny):

x_12= 8,43725 - 1,072i +- sqŕt (-98,66716486-5,50602i) /-2

potřebuju postup, kterým bych to vyřešil. Vím, že i^2 je - 1 a tím bych
vyřešil to, že když dám ty čísla pod odmocninu, staly by se kladnými
a vypočítalo by se to na kalkulačce (odmocňovat záporné číslo nejde).
Pokud bych dal imaginární i reálný jako kladný (tím by se teda vyřešila ta odmocnina)
tak ale co potom s tím i^2 (i na druhou) ? To bude také pod odmocninou a stane se z něj pouhé ,,i" ?
Mám takovou představu:

x_12= 8,43725 - 1,072i +- sqŕt (98,66716486+5,50602i) i^2 /-2

Nevím jestli je má přestava je správná. Ale jestliže bude pouhé i, pak bych tím násobil imaginárním ,,i" ono reálné 98,6.... ale to bych dostal imaginární číslo.
A co teprve bude s tím imaginárním číslem (5,50...) ?
Pokud by se ono i^2 (až po tom odmocnění) vrátilo zpět na -1, kterým
by se jen reálná a imaginární složka vynásobia a staly by se opět jako na začátku
zápornými, pak to není problém. Prostě nevím jak postupovat dál a jak to také bude se znaménky.
Prosím o pomoc, dost to spěchá (ve vzorcích by to bylo přehlednější, ale i za věty budu moc rád)

O čísla mi nejde, jde mi o tu odmocninu se zápornými čísly a ,,i", tedy jak postupovat?

Děkuji předem

BakyX · 29. 09. 2010 23:20

Tu je ukážka, ako sa to počíta. S tvojími číslami to však bude problém. Nedáš sem prosím pôvodne zadanie príkladu s pôvodnými hodnotami vyjadrenými napríklad odmocninami ? Ďakujem

gladiator01

Ahoj, tvůj projev je dost zmatený. Nechtěl by jsi sem napsat původní rovnici, ze které jsi dosazoval do vzorce? Třeba by ti pak někdo snáze poradil.

Možná by ti pomohlo toto (poslední téma na stránce).

martin2z

Děkuji za pomoc. S mými číslami ale asi bude fakt problém, přikládám proto tedy původní čísla a vzorce:
f (e-N/e+2.N)/(e+2N) + (1-f).m-N/m+2.N = 0
f = 0,5
e = -15,874-2,144i
m = 1,00055
N je neznámá

Po dosazení tedy mám:
0,5 (-15,874-2,144i-N)/(-15,874-2,144i+2.N)+0,5.(1,00055-N)/(1,00055+2.N) = 0

Tak z tohoto jsem měl vyjádřit N a vyšlo mi pro kvadratickou rovnici:
(* je zde násobení)

a = (-2*2*0,5)*(-15,874-2,144i)
b = (-1,00055*0,5+2*0,5*(-15,874-2,144i)+(15,874+2,144i) + 0,5*(-15,874-2,144i)+2*1,00055+2*1,00055*0,5)
c = 1,00055

Celý diskriminant mi tedy vyšel
D = (-1,00055*0,5+2*0,5*(-15,874-2,144i)+(15,874+2,144i) + 0,5*(-15,874-2,144i)+2*1,00055+2*1,00055*0,5)2 – 4*(-2*2*0,5)*(-15,874-2,144i)*1,00055=
= (-5,435625-1,072i)2 – 8* (-15,874-2,144i)*1,00055 =
= (-5,435625)*(-5,435625) – (-1,072)*(-1,072) + (-5,435625)* (-1,072)i + (-1,072)i*(-5,435625) -
8*(-15,883 – 2,145i) = 29,54601914 – 1,149184 + 2. 5,82699i -127,064-17,16i =
=28,39683514 + 11,65398i – 127,064-17,16i =
= -98,66716486 – 5,50602 i

Pokud byste to chtěl někdo zkontrolovat a pomoc mi s kořeny právě tohoto hrozného diskriminantu, budu velmi rád.

gladiator01

Není ten vzorec spíš takto? 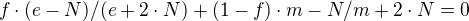$f\cdot (e-N)/(e+2\cdot N)+(1-f)\cdot m-N/m+2\cdot N = 0$ Takto by odpovídal tvému dosazení.
(Místo 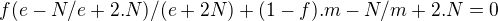$f(e-N/e+2.N)/(e+2N) + (1-f).m-N/m+2.N = 0$ )

A jestli máš dobře to dosazení (chybí ti tam pravá závorka), tak mi ty koeficienty po zjednodušení vycházejí jinak.

Pokud byste to chtěl někdo zkontrolovat a pomoc mi s kořeny právě tohoto hrozného diskriminantu, budu velmi rád.

Když tak "této hrozné rovnice" a ne diskriminantu.

martin2z

gladiator01: ano, máš úplnou pravdu. Ten vzorec je jak jsi ho popsal. Jestli máš někde rozepsanej ten příklad, uvítal bych ho (i číselně). Chybu v závorce odstraňuji. Děkuji mnohokrát.

Jinak jeden kamarád poradil to, co je v tom odkazu (ale bez sin a cos, což bych byl radši a říkal, abych před druhou odmocninu diskriminantu v absolutní hodnotě dal ,,i" a pak ho (po odmocnění diskriminantu tím vynásobil), čímž by z diskriminantu zbyly 2 imaginární čísla (reálné by se přeměnilo na imaginární).

gladiator01 · 30. 09. 2010 13:00

Tak to mam asi špatně, toto nemůžeš napsat pořadně rovnou? Takhle?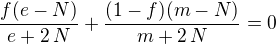
${\frac {f(e-N)}{e+2\,N}}+{\frac {(1-f)(m-N)}{m+2\,N}}=0$
!Když píšeš zlomek (nebo násobení), tak musíš čitatel i jmenovatel (resp. členy, které násobíš) uzávorkovat, aby bylo jasné co do zlomku (resp. co se násobí s čím)patří!

gladiator01 · 30. 09. 2010 14:32

jestli jsem tu tvojí patlanici znova špatně pochopila, tak si mně nepřej

martin2z · 30. 09. 2010 18:05

Díky, díky, díky, díky moc, přesně tohle jsem potřeboval. A Moc se Ti omlouvám, za moji zapomětlivost se znaménky (pospíchal jsem do školy a přehlídl jsem to ve spěchu). Je to má veliká chyba a ještě jednou se omlouvám a mockrát Ti děkuju za pomoc.

Matematické Fórum

#1 29. 09. 2010 21:01 — Editoval martin2z (29. 09. 2010 22:05)

imaginární číslo v řešení kvadratické rovnice

#2 29. 09. 2010 23:20

Re: imaginární číslo v řešení kvadratické rovnice

#3 29. 09. 2010 23:32 — Editoval gladiator01 (29. 09. 2010 23:33)

Re: imaginární číslo v řešení kvadratické rovnice

#4 30. 09. 2010 06:38 — Editoval martin2z (30. 09. 2010 12:35)

Re: imaginární číslo v řešení kvadratické rovnice

#5 30. 09. 2010 11:35 — Editoval gladiator01 (30. 09. 2010 12:34)

Re: imaginární číslo v řešení kvadratické rovnice

#6 30. 09. 2010 12:34 — Editoval martin2z (30. 09. 2010 12:44)

Re: imaginární číslo v řešení kvadratické rovnice

#7 30. 09. 2010 13:00

Re: imaginární číslo v řešení kvadratické rovnice

#8 30. 09. 2010 14:32

Re: imaginární číslo v řešení kvadratické rovnice

#9 30. 09. 2010 18:05

Re: imaginární číslo v řešení kvadratické rovnice

Zápatí