Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 03. 10. 2010 21:02
Indukčnost cívky
Ahoj, mám takový příklad, myslím že vím, jak na něj, ale potřeboval bych se ujistit.
Máme zdroj napětí 9V, cívku o indukčnosti 113*10^-3 H, odpor cívky 20 kOhm. Cívku připojíme k dané baterii (9V), za 17s ji opět odpojíme. Za úkol je zjistit jaké bude maximální napětí a jaký bude maximální proud v obvodu.
Šel jsem na to cestou nejmenšího zla, tudíž jsem si maximální proud vyjádřil jako:  což mi vyšlo
což mi vyšlo  Pak jsem si vyjádřil napětí jako:
Pak jsem si vyjádřil napětí jako:  což mi vyšlo strašně málo, tudíž se Vás ptám, zda-li jsem postupoval správně.
což mi vyšlo strašně málo, tudíž se Vás ptám, zda-li jsem postupoval správně.
Děkuji za pomoc.
Offline
- (téma jako vyřešené označil(a) medvidek)
#2 04. 10. 2010 05:01 — Editoval medvidek (04. 10. 2010 05:07)
Re: Indukčnost cívky
↑ Mathe:
Napětí indukované na cívce je 
Při skokové změně proudu (náhlém přerušení obvodu) dojde teoreticky k nekonečnému nárůstu napětí. Ve skutečnosti ale proud v obvodu neklesne okamžitě. Pokud má obvod nulovou kapacitu, na kontaktech vypínače vznikne alespoň krátce trvající oblouk (jiskra). Energie cívky (přesněji řečeno energie magnetického pole cívky) se při tom ztratí jak v oblouku, tak v reálném odporu cívky. Nebo jsem něco nepochopil? Je potřeba upřesnit, zda se jedná o sériový odpor cívky.
Po připojení baterie se bude proud v obvodu exponenciálně blížit k maximální hodnotě, kterou jsi odhadl správně.
EDIT: Ale také jen za předpokladu, že se jedná o sériový odpor cívky.
Offline
#3 04. 10. 2010 08:46
Re: Indukčnost cívky
Ano, pravděpodobně se jedná o sériový odpor cívky.
Ale nějak nemůžu pochopit, jak dosadit do vzorce, který jsi mi poradil. Je to změna proudu za čas, ale já nevím, jaký bude proud za těch 17s.
Ještě otázka, nešel by tento vzorec zapsat jako: případně +
případně + 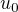
Offline
#4 04. 10. 2010 12:16 — Editoval medvidek (04. 10. 2010 12:17)
Re: Indukčnost cívky
↑ Mathe:
Takhle to zapsat nejde. Zápis je nesprávný i formálně. Jinak integrací proudu v čase bychom mohli vyjádřit náboj kumulovaný na kapacitě kondenzátoru.
Co dosadit do vzorce? No to je právě problém. Od zapojení baterie až do konce 17. sekundy proud monotónně roste a asymptoricky se blíží k hodnotě  . Pak dojde ke skokové změně na nulovou hodnotu a v tomto okamžiku je derivace proudu mínus nekonečno. Tomuto problému se podle mne nevyhneme, dokud nepřipustíme, že obvod má nenulovou kapacitu, anebo že vypnutí nebylo okamžité.
. Pak dojde ke skokové změně na nulovou hodnotu a v tomto okamžiku je derivace proudu mínus nekonečno. Tomuto problému se podle mne nevyhneme, dokud nepřipustíme, že obvod má nenulovou kapacitu, anebo že vypnutí nebylo okamžité.
Pokud by ten odpor cívky byl myšlen jako paralelní, úloha by měla "slušné" řešení. Vlastně i proto jsem se dožadoval upřesnění.
Offline
#6 05. 10. 2010 05:31 — Editoval medvidek (05. 10. 2010 05:52)
Re: Indukčnost cívky
↑ Mathe:
Právě naopak. Je to dobré pro tebe, protože úloha má řešení, špatné pro mne, protože jsem se zabýval něčím, co nebylo potřeba.
Místo reálné cívky v obvodu si představíme ideální cívku PARALELNĚ spojenou s odporem. Obecně platí, že na paralelně zapojených el. součástkách je vždy stejné napětí. Víme tedy, že po celou dobu experimentu bude na odporu napětí stejné jako na cívce.
První část:
Podívejme se nejdřív, jaké budou průběhy napětí a proudů v čase  , kde
, kde  :
:
Napětí budou stejná jako na zdroji  ,
,
proud protékající odporem je dán Ohmovým zákonem  .
.
Pro cívku platí již dřív zmíněný známý vztah  , z kterého přímo plyne
, z kterého přímo plyne  .
.
Objevila se nám tam integrační konstanta, ale protože víme, že v čase t=0 byl proud tekoucí cívkou nulový, můžeme napsat výsledek:
V čase  je průběh proudu cívkou lineární
je průběh proudu cívkou lineární  .
.
Druhá část:
V okamžiku  zdroj odpojíme. Od této chvíle je náš obvod tvořen pouze odporem a cívkou.
zdroj odpojíme. Od této chvíle je náš obvod tvořen pouze odporem a cívkou.
Obecné vztahy pro napětí na odporu a cívce už známe, tato napětí jsou si v daném zapojení rovna:
Nyní jsou i proudy stejné  .
.
Když vyloučíme z rovnic proměnnou  :
:  ,
,
po menší úpravě  .
.
Dostali jsme lin. dif. rovnici 1. řádu, která má řešení ve tvaru
Konstantu A dostaneme z počáteční podmínky, která je daná tím, že v čase  musí průběh proudu spojitě navázat na řešení z první části úlohy, neboli
musí průběh proudu spojitě navázat na řešení z první části úlohy, neboli  .
.
To je splněno, když 
Maximální hodnoty:
Maximální proud v obvodu je ten, který teče ze zdroje napětí těsně před jeho odpojením:
Maximální napětí v obvodu bude na odporu těsně po odpojení zdroje napětí:
Edit: nevýznamná úprava textu
Offline