Matematické Fórum

Zdravím, v některých bodech nesouhlasím.

A) Co třeba ? Přijde mi to jako docela netriviální lineární kombinace.

B) Jaké jsou vektory 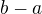a ?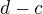

C) (EDIT: Tady jsem se přehlédl, mám to špatně.) Vzhledem k tomu, že , je lineární závislost zřejmá.

↑ LukasM:
Díky za upozornění.

↑ blanvan:
A) ano, netriviální lineární kombinace, která je rovna nulovému vektoru skutečně existuje, jak už ukázal Olin někde výše. Ten postup je ale zvláštní.

B) ano, pak se nám pochlub s postupem

C) netriviální lineární kombinace, která je rovna nulovému vektoru skutečně neexistuje. Ke tvému zdůvodnění se ale radši nebudu vyjadřovat.


vyrobím ti teď ještě příklad D) : vektory budou ((1,0,0,0),(0,1,0,0),(1,1,0,0),(0,0,0,1)) - a jsem zvědaný nejen na výsledek, ale i na postup. Bylo by dobré fakt to oskenovat (jak jsem ti radil někde ve vedlejším vlákně), nebo tady podrobně popsat, ať se posuneme dál.

↑ blanvan:
Tak jo.

A) Soubor ((0,0,0),(1,1,1)) je opravdu lineárně závislý. Tvoje zdůvodnění ale nedává smysl.
O co nám při tom zjišťování LN/LZ vůbec jde? Zkoumáme, jak se z těch vektorů dá nakombinovat nulový vektor. Pokud je jediná možnost jak to udělat tak, že všechny vektory vynásobíme nulou a pak sečteme, je soubor LN. Pokud se nulový vektor dá nakombinovat jakkoli jinak, je soubor LZ.

V našem případě řešíme, jestli rovnost 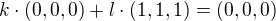platí pouze pro (to pak platí určitě, to je snad jasné - neboli triviální, odtud taky ten termín triviální nulová kombinace), nebo jestli jde najít takovou dvojici k,l, že alespoň jedno z nich je nenulové, a přitom rovnost platí (netriviální nulová kombinace).
Tady je na první pohled vidět, že rovnost platí pro l=0 nezávisle na k. Odtud vidíme, že nulový vektor lze nakombinovat i netriviálně, a soubor je tedy LZ.


C) "netriviální nulová kombinace neexistuje a vektory jsou nezávislé" - ano, je to přesně tak. Jen budu nadávat za to tvoje "hodím to do matice". Proč? Ta matice není nic jiného, než nějak úsporně zapsaná soustava rovnic. Oba postupy jsou naprosto ekvivalentní, akorát u jednoho nepíšeš ty písmenka co označujou neznámé a plusy mezi to. Opět je za tím schované totéž co u bodu A), tedy že zkoumáme, jak z těch vektorů nakombinovat nulový vektor. Tj. řešíme následující problém: hledáme k,l,m tak, aby platilo:
.

Zdánlivě jedna rovnice pro tři neznámé, ale můžeme si to rozepsat po složkách vektorů. Musí tedy platit: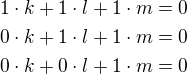


Tahle soustava je jednoduchá, je vlastně už vyřešená (jediné řešení k=l=m=0). Teď tedy můžeme říct, že jediná možnost jak z vektorů nakombinovat nulový vektor je triviálně, a soubor je LN.
Je opravdu důležité si uvědomovat, že ta úprava matice soustavy na schodovitý tvar není nic jiného než sčítání rovnic tak, abychom se dostali k řešení. Jestli tam píšu matici, nebo tři rovnice pod sebe je jedno.


A ještě poznámku k tomu "snažila jsem se to počítat jako rovnice, ale dosazení do matice je jednodušší" - je to stejné, to jsem právě vysvětlil. Ale když se podíváš pořádně, tak zjistíš, že ty rovnice které jsi původně psala jsou jiné než ty, které jsi teď přepsala ve formě matice. Matice soustavy kterou jsi psala původně by vypadala takhle:

Jak vidíš, je to soustava pro dvě neznámé místo tří, a nemá vůbec žádné řešení. Tys tam všude jeden z těch vektorů psala na pravou stranu, což je ale špatně, všechny vektory se něčím násobí. Takže to není tím že matice jsou lepší než do detailů rozepsané soustavy - je to o tom, napsat tu soustavu správně. Jestli ji pak napíšu ve formě matice nebo ne, je úplně jedno.



B) To je přesně to co jsem právě popsal, akorát ta soustava není hned vyřešená, ale je potřeba ji vyřešit. Pokud bude mít pouze triviální řešení, je soubor LN, pokud ne, bude LZ. Pak se pochlub s postupem.

D) To je špatně, soubor je LZ - třetí vektor je součet prvního a druhého, takže nulový vektor nakombinuju snadno. Třeba tak, že první dva vektory vynásobím jedničkou, třetí -1čkou a poslední nulou. To mi po součtu dá určitě nulový vektor, i když koeficienty nejsou všechny nulové. Ale příklad není o tom aby sis tohohle hned všimla - pořádným a správným vyřešením soustavy rovnic (kterou si sestavíš) se k tomu závěru dostaneš.


A ještě kontrolní domácí úkol - mám soubor 4 vektorů z 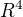(tedy nějaké čtveřice, jako u toho příkladu D). Jak nejrychleji dokážeš tvrzení, že pokud jsou dva z nich stejné, je celý soubor určitě LZ? (O tohle tvrzení se právě opíral Olin, když se tě ptal jaké jsou vektory b-a a d-c).

D) ano

B)
1. způsob je v pořádku

2. způsob je úplná blbost. Za prvé - když píšeš "...tak bych podle této podmínky hned vim, že jsou lineárně závislé", o jaké podmínce mluvíš?
Dál - jak jsi ze soustavy čtyř rovnic jen tak udělala soustavu dvou rovnic? Vždyť jsi zapomněla opsat 1. a 3. řádek, ty nemůžou z té soustavy jen tak zmizet. Soustava je přirozeně stejná jako v prvním způsobu. Ty dvě rovnice které ti tam zbyly jsou přece ty, o kterých jsi v 1. způsobu řekla, že "3. a 4. řádek jsou pouze násobkem 2. řádku, tak už je dál neopisuju". Nevím co tě vedlo k těmhle úpravám.. Olin se původně ptal: "Jaké jsou vektory 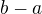a 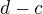?" Co chtěl teda vůbec slyšet jako odpověď?

Navíc si můžeš snadno ověřit, že a+b-c-d rozhodně nedají nulový vektor, a že to tedy těžko může být dobře. Schválně sem napiš kolik číselně vyjde součet a+b-c-d.

↑ blanvan:
V zásadě by se na to tak dívat dalo, jen je potřeba si ujasnit, jak tedy bude vypadat ta hledaná nulová netriviální kombinace. Pokud b-a a d-c jsou stejné vektory, vidíme to z hlavy. Netriviální kombinace je např. (b-a)-(d-c)=-a+b+c-d - tak to musí být, protože ty dvě závorky tam jsou dva stejné vektory (což je podle mně to slovo, které chtěl slyšet Olin), takže odečtu-li jeden od druhého, dostanu nulový vektor.

Pokud mám v souboru dva vektory stejné, dá se argumentovat vlastně stejně. Jeden z nich vynásobím nenulovým číslem, ten druhý číslem opačným, všechny ostatní nulou - potom bude součet nulový vektor, a přesto budou dva koeficienty lineární kombinace nenulové.