Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » důkaz, diskrétní matematika (TOTO TÉMA JE VYŘEŠENÉ)
#1 04. 10. 2010 21:10
důkaz, diskrétní matematika
Ahoj, mohl by mi někdo poradit (a vysvětlit) řešení tohoto příkladu? Děkuju, byla bych moc vděčná
Nechť n je z množiny přirozených čísel (N). Dokažte, že mezi n+1 vybranými čísly z množiny {1,2,3.....2n} existuje dvojice a, b (a se nerovná b) tak, že a dělí b.
Physics isn't the most important thing. Love is. Best wishes, Richard Feynman
Offline
- (téma jako vyřešené označil(a) Esperance)
#2 04. 10. 2010 22:11
Re: důkaz, diskrétní matematika
Jde o poměrně trikovou záležitost - je chytře využit tzv. Dirichletův princip (triviální pozorování, že když deset aut vjelo do devíti garáží, tak v nějaké garáži musí být aspoň dvě). Za tímto účelem doporučuji rozdělit množinu 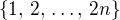 na množiny
na množiny 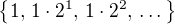 ,
, 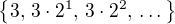 až po
až po 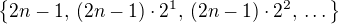 (všechny tyto množiny jsou podmnožiny
(všechny tyto množiny jsou podmnožiny 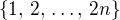 , které s lichým číslem obsahují i všechny jeho možné násobky mocninou dvojky).
, které s lichým číslem obsahují i všechny jeho možné násobky mocninou dvojky).
Offline
#3 05. 10. 2010 19:10
- check_drummer

- Příspěvky: 5184
- Reputace: 106
Re: důkaz, diskrétní matematika
Rozdělme množinu {1,..,2n} na dvojice {i,2i} (i<=n). Dvojic je n, tedy při výběru n+1 čísel jistě nějaké dvě čísla padnou do stejné dvojice j,2j, což jsou hledaná a,b.
"Máte úhel beta." "No to nemám."
Offline
#4 05. 10. 2010 19:14
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: důkaz, diskrétní matematika
↑ check_drummer:
Dvojic je sice n, ale nepokrývají celou množinu. Např. 2n-1 nebude v žádné dvojici.
Offline
#5 05. 10. 2010 21:23
- check_drummer

- Příspěvky: 5184
- Reputace: 106
Re: důkaz, diskrétní matematika
↑ BrozekP:
Je to tak, dvojice totiž nejsou disjunktní, jak jsem si u večeře uvědomil. :-)
"Máte úhel beta." "No to nemám."
Offline
#6 05. 10. 2010 21:30
- check_drummer

- Příspěvky: 5184
- Reputace: 106
Re: důkaz, diskrétní matematika
↑ Olin:
Jen formálně - poslední množina bude pro n>1 obsahovat jediné číslo 2n-1 - totiž (2n-1).2 > 2n.
"Máte úhel beta." "No to nemám."
Offline
#7 05. 10. 2010 21:35
Re: důkaz, diskrétní matematika
↑ check_drummer:
To je samozřejmě pravda a takovýchto množin bude více. Mám-li zapsat přesně, o jaké množiny jde, pak půjde o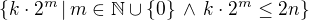
kde 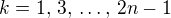 .
.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » důkaz, diskrétní matematika (TOTO TÉMA JE VYŘEŠENÉ)