Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 06. 10. 2010 15:26
- Progresive
- Příspěvky: 85
- Reputace: 0
Variace
Zdravím, můžu se zeptat jak vypočtu tyto úlohy? nemůžu zaboha přijít na způsob ;)
Z kolika různých prvnků lze vytvořit 13800 variací třetí třídy?
Zvětšíme-li počet prvků o jeden, zvětší se počet variací druhé třídy bez opakování o 16. Určtete původní počet prvků.
Určete počet prvků, je-li počet variací čtvrté třídy bez opak. dvacetkrát větší než počet variací druhé třídy bezopak.
Kolik různých prvků dá 22350 variací druhé třídy bez opak?.
Offline
- (téma jako vyřešené označil(a) jelena)
#3 06. 10. 2010 15:43
Offline
#4 06. 10. 2010 15:45
Offline
#5 06. 10. 2010 15:55
- Progresive
- Příspěvky: 85
- Reputace: 0
Re: Variace
Díky! Druhý už je mi tedy jasný ten jsem mezitím už zpočítal také. Ale i když si spočítám tu 1( i 4) a 3 tak mi to prostě nevychází jak má.. Asi špatně počítám. Mohl by jste mi prosím ještě vzorově spočítat příklad 1 a 3? Díky moc
Offline
#6 06. 10. 2010 16:06
Offline
#7 06. 10. 2010 16:09
- Progresive
- Příspěvky: 85
- Reputace: 0
Re: Variace
↑ b.r.o.z1:
asi jsem se špatně vyjádřil, toto chápu... ale "n" má vyjít 25 .. a já mám někde početní chybu a nevím kde ;) neumím upravovat asi ;) ..
Offline
#8 06. 10. 2010 16:23
Re: Variace
↑ Progresive:
CO tam počítáš???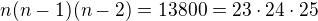
na levé straně je součin tří za sebou jdoucích čísel a na pravé taky. Takže to největší na levé straně ( ) je rovno tomu největšímu na pravé (
) je rovno tomu největšímu na pravé ( ).
).
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#9 06. 10. 2010 16:26
- Progresive
- Příspěvky: 85
- Reputace: 0
Re: Variace
↑ zdenek1:
jak zjistím že to je právě těch 25..?
Offline
#11 06. 10. 2010 17:55
Re: Variace
↑ johny239:
No tak vidím 13800=138*100
dál znám kritéria dělitelnosti, takže vidím, že 138 je dělitelné šesti (ciferný součet dělitelný třemi a je sudé). takže jsem si vydělil 138:6=23.
A taky vím, že 100=4*25.
Tak mám 13800=23*6*4*25
No a to mi stačí
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#12 06. 10. 2010 18:03
Re: Variace
↑ zdenek1:
Ok jasně takže nejde o nic jiného než jsi to upravit na požadovaný tvar a poté si 13800 rozložit podle krytérií z toho výrazu chápu dobře?
Offline
#13 06. 10. 2010 18:10
Re: Variace
↑ johny239:
No jasně. Kdyby tam nebyly ty podmínky, že  atd. jsou přirozená čísla, tak by se musela řešit kubická rovnice, což ale není normální středoškolské učivo. Takže když vidím, že na jedné straně je součin tří za sebou jdoucích přirozených čísel, tak se snažím na druhé straně vytvořit také. Tady to šlo snadno.
atd. jsou přirozená čísla, tak by se musela řešit kubická rovnice, což ale není normální středoškolské učivo. Takže když vidím, že na jedné straně je součin tří za sebou jdoucích přirozených čísel, tak se snažím na druhé straně vytvořit také. Tady to šlo snadno.
Pořádek je pro blbce, inteligent zvládá chaos!
Offline

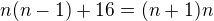

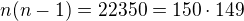
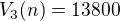
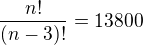
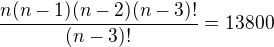
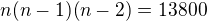 takhle se na to dostal
takhle se na to dostal 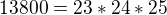 chápu že
chápu že  ale prosím Vás jak jste přisli na ten rozklad
ale prosím Vás jak jste přisli na ten rozklad 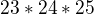 a tedy že
a tedy že