Matematické Fórum

blanvan · 08. 10. 2010 12:05

Ahoj :) potřebovala bych pomoct s tímto příkladem. Už jsem se o něco pokoušela, ale asi to bude blbost..

(sinx + tg5x) / (sin4x + tg2x) = x * sinx/x * 5x * tg5x/5x * 1/4x * 4x/sin4x * 1/2x * 2x/tg2x = x * 5x * 1/4x * 1/2x * sinx/x * 4x/sin4x * tg5x/5x * 2x/tg2x = 2/3

Děkuji moc :)

blanvan · 08. 10. 2010 12:31

Jejda, úplně jsem zapomněl ana označení lim a že x jde k 0.

Pavel Brožek

↑ blanvan:

Správně jsi usoudila, že to není správně :-). Na začátku máš sčítání, ale po prvním kroku násobení – proč?

Spíš bych zkusil celý zlomek krátit sinx.

Tychi · 08. 10. 2010 12:36

jak se ti ze sčítání stalo násobení?

Honzc · 08. 10. 2010 13:16

↑ blanvan:
Spíš bych zkusil L'Hospitalovo pravidlo

blanvan · 08. 10. 2010 13:41

Tak to jsem ráda, že jsem aspoň správně usoudila, že je to blbost :)

Z toho, co jsem vyčetla ze skript a tady na fóru, mi tak nějak vyšlo, že bych se měla pokusit limitu rozložit, aby byl zlomek vždy ve tvaru sinax/ax nebo tgax/ax. To násobení jsem popletla.

A takhle by to mohlo být, že bych si to rozložila na jednotlivé zlomky a pronásobila, aby se pak zlomky s goniometrickými fcemi rovnaly 1?

(sinx + tg5x) / (sin4x + tg2x) = x * sinx/x + 5x * tg5x/5x + 1/4x * 4x/sin4x + 1/2x * 2x/tg2x = 2/3

Krátit sinx? To znamená takhle? : [sinx * (1 + tg5x/sinx)] / [sin4x * (1 + tg2x/sin4x)]

Cheop · 08. 10. 2010 13:42 — Editoval Cheop (08. 10. 2010 13:48)

↑ Honzc:
Myslíš toto?
Tuná

blanvan · 08. 10. 2010 14:06

Super, to je přesně můj příklad...jen ten postup moc nechápu, tak to jdu nabiflovat a snad něco pochopim :)
Děkuji moc moc moc !!!

Rumburak

↑ blanvan:
To, co posílá kolega ↑ Cheop:, je tak trochu kanon na vrabce a vůbec se nedivím, že Ti to není srozumitelné, pokud jste neprobírali
Taylorovy řady. Úprava, která pomůže a kterou radil kolega ↑ BrozekP:, je

$\frac {\sin\,x\, + \,\tan\,5x}{\sin\,4x \,+\, \tan\,2x}\,=\,\frac {\sin\,x\,\cdot\,$1\,+\,\frac{\sin\,5x}{\sin\,x}\cdot \frac{1}{\cos\,5x}$}{\sin\,x\,\cdot\,$\frac{\sin\,4x}{\sin\,x}\,+\,\frac{\sin\,2x}{\sin\,x}\cdot \frac{1}{\cos\,2x}$}$ .

Dále se použije vzorec $\lim_{\small{t \to 0}} \frac{\sin\,t}{t} = 1$ , pomocí něhož se spočítají limity tvaru $\lim_{\small{x \to 0}} \,\frac{\sin\,ax}{\sin\,bx}$ pro $b \ne 0$ .

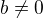EDIT. Ještě o chlup lépe by to řešila úprava

$\frac {\sin\,x\, + \,\tan\,5x}{\sin\,4x \,+\, \tan\,2x}\,=\,\frac {x\,\cdot\,$\frac{\sin\,x}{x}\,+\,\frac{\sin\,5x}{x}\cdot \frac{1}{\cos\,5x}$}{x\,\cdot\,$\frac{\sin\,4x}{x}\,+\,\frac{\sin\,2x}{x}\cdot \frac{1}{\cos\,2x}$}$ ,

Pro $a\ne 0$ je $\lim_{\small{x \to 0}} \,\frac{\sin\,ax}{x}= a\cdot \lim_{\small{x \to 0}} \,\frac{\sin\,ax}{ax}= a\cdot 1 = a$ .

Cheop · 08. 10. 2010 14:41 — Editoval Cheop (08. 10. 2010 14:46)

↑ blanvan:
L'Hospital
Uděláš to prostě tak, že zvláštˇzderivuješ čitatele a zvlášť jmenovatele lomené funkce
a potom do této derivace dosadíš znovu to k čemu se ta limita blíží
Pro tvůj případ:
Derivace čítatele $(\sin(x)+\rm{tg}(5x))^'=\cos(x)+\frac{5}{\cos^2(5x)}$
Derivace jmenovatele: $(\sin(4x)+\rm{tg}(2x))^'=4\,\cos(4x)+\frac{2}{\cos^2(2x)}$
Dostaneme tedy:
$\lim_{x\rightarrow0}\,\cdots\,\cdots\,=\lim_{x\rightarrow0}\,\frac{\cos(x)+\frac{5}{\cos^2(5x)}}{4\,\cos(4x)+\frac{2}{\cos^2(2x)}}=\frac{\cos(0)+\frac{5}{\cos^2(0)}}{4\cdot\cos(0)+\frac{2}{\cos^2(0)}}=\frac{1+\frac{5}{1}}{4+\frac{2}{1}}=\frac 66=1$

Cheop · 08. 10. 2010 14:43

↑ Rumburak:
Zdravím
Příspěvek 10 už snad jako "kanón na vrabce" nevypadá?

Pavel Brožek · 08. 10. 2010 14:53

↑ Cheop:

Nevypadá to tak šíleně složitě, ale je to pouze tím, že ty (narozdíl od Wolfram|Alpha) nevypisuješ každou úpravu provedenou podle aritmetiky limit a vět o limitě složené funkce. Stále je to kanón na vrabce – l'Hospital zde není potřeba :-).

Cheop · 08. 10. 2010 14:56

↑ BrozekP:
Dobře já se vzdávám.
Ať si to tazatel spočítá jak chce.

Rumburak

↑ Cheop: O.K. Samozřejmě neškodí, když tazatel je seznámen s různými metodami, ale ty základní by chybět neměly,
proto jsem doplnil, co mi připadalo, že by tam být mělo určitě. Zdravím též.

blanvan · 08. 10. 2010 15:33

Všem moc děkuji!!Teď už se mi to zdá srozumitelnější :) L´Hospitala se budu učit za chvíli, ale docela dobře jsem to, jak je to rozepsané, pochopila. Jen myslim, že se po mně chce, abych to vypočítala klasickou metodou. Zkoušela jsem to tedy dopočítat tou základní cestou a došla jsem k tomuto:

[x * (1 + 5 * sin5x/5x * 1/cos5x)] / [ x * (4 * sin4x/4x + 2 * sin2x/2x * 1/cos2x)]

Pak tedy použiji vzorec sinax/ax = 1... jen nevim, jestli 1/cosax = 1? - počítala jsem, že je rovno 1.

[x * (1 + 5 * 1 * 1)] / x * (4 * 1 + 2 * 1 * 1)] = 6/6 = 1

Je to správně nebo se alespoň přibližuji ke správnému postupu? :)

Rumburak

↑ blanvan:
Ano, takto je to správně. Funkce cos x v celém R a tedy i v bodě x = 0 spojitá a cos 0 = 1, tímto a větou o limitě složené funkce
je odůvodněna správnost Tvé úvahy o limitě funkce 1/cosax .

PS. To vytknuté x se samozřejmě (hned) vykrátí, takže v tom výrazu [x * (1 + 5 * 1 * 1)] / x * (4 * 1 + 2 * 1 * 1)]
vzniklém provedením limity by už figurovat nemělo.

blanvan · 08. 10. 2010 16:12

Zdálo se mi to hrozně složitý, ale takhle už to nevypadá tak strašidelně :) tak jdu zkusit i ostatní příklady a doufám, že něco vypočítám :)

Děkuji moc !!!!

Matematické Fórum

#1 08. 10. 2010 12:05

limita funkce

#2 08. 10. 2010 12:31

Re: limita funkce

#3 08. 10. 2010 12:34 — Editoval BrozekP (08. 10. 2010 12:35)

Re: limita funkce

#4 08. 10. 2010 12:36

Re: limita funkce

#5 08. 10. 2010 13:16

Re: limita funkce

#6 08. 10. 2010 13:41

Re: limita funkce

#7 08. 10. 2010 13:42 — Editoval Cheop (08. 10. 2010 13:48)

Re: limita funkce

#8 08. 10. 2010 14:06

Re: limita funkce

#9 08. 10. 2010 14:33 — Editoval Rumburak (08. 10. 2010 15:02)

Re: limita funkce

#10 08. 10. 2010 14:41 — Editoval Cheop (08. 10. 2010 14:46)

Re: limita funkce

#11 08. 10. 2010 14:43

Re: limita funkce

#12 08. 10. 2010 14:53

Re: limita funkce

#13 08. 10. 2010 14:56

Re: limita funkce

#14 08. 10. 2010 14:58 — Editoval Rumburak (08. 10. 2010 15:10)

Re: limita funkce

#15 08. 10. 2010 15:33

Re: limita funkce

#16 08. 10. 2010 15:58 — Editoval Rumburak (08. 10. 2010 16:07)

Re: limita funkce

#17 08. 10. 2010 16:12

Re: limita funkce

Zápatí