Matematické Fórum

JardaB · 06. 10. 2010 16:56

Zdravím vás,

potřeboval bych pomoc s následujícím.

Mám dokázat, že funkce $n^k$ = $o(c^n)$ , kde k je libovolné celé číslo a c > 1.

o(f(n)) je definovano nasledovne:
$o(f(n)) = \{g(n) : \forall c > 0 : \exists n_0 \in N+ : \forall n >= n_0 : g(n) <= c * f(n)\}$

Já to chápu tak, že musím dokázat, že fce $n^k$ roste vždy pomaleji než fce $c^n$

Poradíte mi, prosím, jak? Jestli přes limity nebo jinak...

Díky moc předem

Pavel · 06. 10. 2010 18:00

↑ JardaB:

$\lim_{n\to\infty}\frac{n^k}{c^n}=0,\qquad k\in\mathbb{R},\ c>1.$

Olin · 06. 10. 2010 18:07

Pak je ještě třeba si uvědomit (dokázat), že limita podílů nám již říká vše ve smyslu uvedené definice symbolu o.

JardaB · 06. 10. 2010 18:29 — Editoval JardaB (06. 10. 2010 18:32)

↑ Pavel:

Děkuju.
Nebyla by, prosím, nějaká nápověda řešení?
Umím řešit akorat jednoduché limity.

Pavel · 09. 10. 2010 13:35 — Editoval Pavel (09. 10. 2010 14:20)

↑ JardaB:

Nechť k je celé číslo a c>1.

1. předpokládejme, že k je záporné nebo nulové. pak můžeme psát

$\lim_{n\to\infty}\frac{n^k}{c^n}=\lim_{n\to\infty}\frac{1}{n^sc^n}=\frac{1}{\infty\cdot\infty}=0,\qquad s=-k$ .

2. předpokládejme, že k je kladné. Pak limitu můžeme řešit pomocí k-násobného použítí l'Hospitalova pravidla

$\lim_{n\to\infty}\frac{n^k}{c^n}=\lim_{n\to\infty}\frac{kn^{k-1}}{c^n\cdot\ln c}=\lim_{n\to\infty}\frac{k(k-1)n^{k-2}}{c^n\cdot\ln^2 c}= \lim_{n\to\infty}\frac{k(k-1)(k-2)n^{k-3}}{c^n\cdot\ln^3 c}=\dots=\lim_{n\to\infty}\frac{k(k-1)(k-2)\cdots 2\cdot 1}{c^n\cdot\ln^k c}=\frac{k!}{\infty}=0$ .

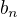To že limita podílu obou posloupností stačí k tomu, abychom prohlásili, že $n^k=o(c^n)$ , vyplývá z toho, že limita jejich podílu (viz výše) rovná se 0. Stačí jenom uvážit, že jsou-li posloupnosti $a_n$ a $b_n$ kladné, pak

$\lim_{n\to\infty}\frac{a_n}{b_n}=0\quad\Leftrightarrow\quad \forall\varepsilon>0\,\exists n_0\in\mathbb{N}\,:\,\forall n\geq n_0\,:\, \frac{a_n}{b_n}<\varepsilon$

Všimni si, že definice je téměř stejná jako Landauova symbolu 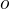$o$ . Poslední nerovnost upravíme $a_n<\varepsilon b_n$ .

JanuraJ · 09. 10. 2010 19:32

řeším stejný příklad a nešlo by to udělat tak že:

$n^k=o(c^n)$
$log(n^k) <= log(c^n)$
$k*log (n) <= n log (c)$
$k (log (n)) / n <= log (c)$
$k*\lim_{n\to\infty}\frac{log n}{n}=0$
a jelikož log má kladný definiční obor tak nikdy nemůže dosáhnout hodnoty 0

JardaB · 10. 10. 2010 00:15

Já jsem to ještě zkoušel přes ty limity a dostal jsem se k tomuhle..

Řeším: $\lim_{x\rightarrow \infty}n^k/c^n$
na to pouziju l"Hospitala...nekolikrat...
tak v citateli dostanu: $k*(k-1)*(k-2)*(k-3).....n^0$
a ve jmenovateli dostanu: $c^n * ln(c) * ln(c)....$

takze v citateli budu mit po spouste kroci vzdy konstantu
a ve jmenovateli dostanu $c^\infty * ln(c) * ln(c)... = \infty$

takze budu mit $\lim_{x\rightarrow \infty}konstanta/\infty=0$

nebo je to uplne blbe?

Pavel · 10. 10. 2010 10:08 — Editoval Pavel (10. 10. 2010 10:10)

↑ JanuraJ:

Myšlenka je v pořádku, jen je potřeba při úpravách pracovat s nerovností

$\log(n^k)\leq\log(\alpha c^n)$ (v definici "malého o" je to konstanta c, ale tu tady použít nemůžu, tak jsem zvolil $\alpha$ ) a dokázat tuto nerovnost pro všechna kladná $\alpha$ . Stejná technika, kterou jsi použil, by měla fungovat i na tuto nerovnost.

↑ JardaB:

Přesně to jsem použil ve svém předchozím příspěvku. Jen si musíš dát pozor, že l'Hospitalovo pravidlo můžeš použít jen, když $k$ je kladné. V opačném případě dostaneš limitu vedoucí na výraz $1/\infty$ .