Matematické Fórum

ators · 11. 10. 2010 17:00 — Editoval ators (11. 10. 2010 17:25)

Ahojte mám trojuhelnik pravouhly... přepona je 100 cm (ta nejdelsi strana) zbyle dve maji stejnou délku...
pomocí pyth věty.. > c2=a2+b2

potřebuju zjistit jakou delku ma jedne z menších stran

nemám tohle dobře??

100 (na druhou) je 10000
10000 : 2 = 5000
5000 (odmocnina 2) =70,7106...

Ale to není správně :'( tak jak??

Lépe řešeno jestli to dělám vůbec správně :( napíši raději celé zadání !! >>

Krychle
telesová uhlopřička je 100 cm?

povrch=?
objem=?

povrch má být 192450cm2

b.r.o.z1

ahoj, ty vlastně znáš u, snažíš se získat stranu a, u1 se dá dopočítat snadno:-)
$u_1=\sqrt{2}a$
$u^2=u_1^2+a^2$
$100^2=2a^2+a^2$
$sqrt{\frac{10000}{3}}=a$

ators · 11. 10. 2010 17:24

pořád nechápu proč je tu tohle :( $100^2=2a^2+a^2$

b.r.o.z1 · 11. 10. 2010 17:32

↑ ators:
podívej se na obrázek kudy vede tělesová úhlopříčka(ozn. u), společně s 1x stranou a a 1x úhlopříčkou v podstavě (u_1) tvoří trojúhelník
úhlopříčka v podstavě u_1 se vypočítá pomocí Pythagorovy věty: $u_1^2=a^2+a^2$ $u_1=\sqrt2a^2$

ators · 11. 10. 2010 18:37 — Editoval ators (11. 10. 2010 18:38)

Omlouvám se , ale co je $u_1^2$ ?

A nažím se vypočítat povrch a objem takže potřebuji a a ne u , ne?

InFlamer · 11. 10. 2010 18:43

↑ ators:
u1 na druhou, ne ta tělesová, ale stěnová úhlopříčka, jak ma b.r.o.z1 v tom obrazku.

ators · 11. 10. 2010 18:44

však ano, ale já potřebuji stranu a ne??

LukasM · 11. 10. 2010 18:44 — Editoval LukasM (11. 10. 2010 18:45)

↑ ators:
Druhá mocnina délky úhlopříčky podstavy, viz. obrázek výše. Kolega ↑ b.r.o.z1: tam nicméně má chybku, správně má být závěr 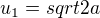$u_1=sqrt{2}a$ - v tom příspěvku s obrázkem je to ale správně.

Od začátku. Aby ses dostal od tělesové úhlopříčky ke straně, musíš dvakrát aplikovat Pythagorovu větu. Nejdřív na trojúhelník tvořený půlkou podstavy (abys zjistil výše uvedený vztah mezi $a$ a 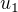$u_1$ ), a podruhé na trojúhelník tvořený (podle obrázku) stranami $a,u_1,u$ (který je bezpochyby také pravidelný) - to je právě to $100^2=2a^2+a^2$ . Dává to smysl?

ators · 11. 10. 2010 19:03

Ano,
to celé chápu.
Ale jak zjístím kolik měří u1, a ?
$2a^2$ a proč je tohle? nestačí to takto? $a^2$
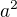
Omlouvám se ale tohle je první co takle nechápu :'(

Spybot · 11. 10. 2010 19:40

Tak este raz:

Mame stranu $a$ . Z Pyt. vety: $a^2+a^2=u^2_1=2a^2 \Rightarrow u_1=\sqrt{2}a$

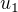Teraz pouzijeme Pyt. vetu po druhykrat. $u_1^2+a^2=u^2$ Ale $u_1$ sme uz vyjadrili, preto dosadime.
$(\sqrt{2}a)^2+a^2=u^2$

A uz Ti to hadam pojde.

Honzc · 12. 10. 2010 06:05 — Editoval Honzc (12. 10. 2010 06:06)

↑ ators:
Nevím nevím, ale ten tvůj výsledek pro povrch se mi nějak nelíbí, nejspíš bude špatně.
Mně vychází P=2*u^2

Matematické Fórum

#1 11. 10. 2010 17:00 — Editoval ators (11. 10. 2010 17:25)

Pythagorova věta

#2 11. 10. 2010 17:10 — Editoval b.r.o.z1 (11. 10. 2010 17:12)

Re: Pythagorova věta

#3 11. 10. 2010 17:24

Re: Pythagorova věta

#4 11. 10. 2010 17:32

Re: Pythagorova věta

#5 11. 10. 2010 18:37 — Editoval ators (11. 10. 2010 18:38)

Re: Pythagorova věta

#6 11. 10. 2010 18:43

Re: Pythagorova věta

#7 11. 10. 2010 18:44

Re: Pythagorova věta

#8 11. 10. 2010 18:44 — Editoval LukasM (11. 10. 2010 18:45)

Re: Pythagorova věta

#9 11. 10. 2010 19:03

Re: Pythagorova věta

#10 11. 10. 2010 19:40

Re: Pythagorova věta

#11 12. 10. 2010 06:05 — Editoval Honzc (12. 10. 2010 06:06)

Re: Pythagorova věta

Zápatí