Matematické Fórum

hradecek · 06. 10. 2010 17:51

Ahoj,
Mám štvorec ABCD kde A=[-1;3] a B=[-8;4] a chcem vypočítať bod C=[x;y].
A nie som si úplne istý ako na to...

Je jasné, že môžu byť dve možnosti kde sa bude bod C nachádzať.
Ja som si najprv vypočítal vektor $\vec{AB}=(-7;1)$ a vlastne ak ho otočíme z bodu B o 90° dostaneme bod C...
A dostal som sa k výsledkom C=[7;11] a C'=[-9;-3]

Ale príde mi to také nematematické, dá sa to inak ? a je to vôbec správne ?

Dík.

zdenek1 · 06. 10. 2010 18:06

↑ hradecek:

$C[-7;11]$

jinak dobře.

Já bych to jinak nedělal.

hradecek · 06. 10. 2010 18:24

↑ zdenek1:
No veď práve, vravím, že ani mne sa to moc nepáči...ale ešte nie som v analytickej geometrii taký zbehlý ;)
A môžem vedieť ako by si to robil ty ?

hradecek · 13. 10. 2010 19:41

Vedel by niekto iný postup ?

medvidek · 14. 10. 2010 00:15

↑ hradecek:
Riešil by si dve rovnice o dvoch neznámych.
Prvú (lineárnu) dostaneš z podmienky kolmosti vektorov 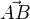$\vec{AB}$ a $\vec{BC}$ . Skalárny súčin je nulový:
$\vec{AB} \cdot \vec{BC}=0$
Druhú (kvadratickú) dostaneme z podmienky rovnosti veľkosti vektorov:
$|\vec{AB}|=|\vec{BC}|$
Z toho vyplynú dve možnosti pre vektor $\vec{BC}$ , a teda i pre bod $C$ .

Cheop · 14. 10. 2010 08:16 — Editoval Cheop (14. 10. 2010 14:32)

↑ hradecek:
Způsob 3)
Vzdálenost AB $\sqrt{(-1+8)^2+(3-4)^2}=\sqrt{50}$
Protože se jedná o čtverec pak víme, že úhlopříčka je $u=a\sqrt2=\sqrt2\cdot\sqrt{50}=\sqrt{100}$ (vzdálenost AC)
Pokud označím souřadnice bodu C(x; y) pak lze sestavit rovnice:
1) $\sqrt{(x+8)^2+(y-4)^2}=\sqrt{50}$ - vzdálenost bodu C od bodu B
2) $\sqrt{(x+1)^2+(y-3)^2}=\sqrt{100}$ - vzdálenost bodu C od bodu A
Řešením těchto rovnic je:
$C_1=(-9;\,-3)\nlC_2=(-7;\,11)$

Analogicky pro bod D(x_0; y_0) by platilo:
3) $\sqrt{(x_0+8)^2+(y_0-4)^2}=\sqrt{100}$ - vzdálenost BD
4) $\sqrt{(x_0+1)^2+(y_0-3)^2}=\sqrt{50}$ - vzdálenost AD
Obrázek: