Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 14. 10. 2010 10:48
Lokální extrém funkcí více proměnných
Zdravím,
nevím si trochu rady s výpočtem lokálního extrému funkce, resp. spíše nevím jak v daném příkladě vypočíst body, jenž by byly podezřelé z extrému.
Funkce: 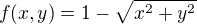
z toho jsem vypočetl parciální derivace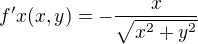
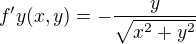
No a z toho nějak nedokážu vydolovat podezřelý bod, zkoušel jsem to i do MAWu strčit a také nic. Ale podle mě když si to trochu představím ten graf, tak když budu mít v 3d osy xyz (z bude výška), tak v souřadnici[0,0,1] to podle mě trochu zavání maximem, ale nejsem si jist. Protože podle mě to těleso bude něco připomínající kužel s tím že v tomto bodě bude vrchol. Čili podezřelý by mohl být možná bod 0,0. Nicméně kdyby byl, tak když spočítám druhé derivace, tak mi vznikne dělení nulou. Tak nevim...
Díky za každou radu.
Offline
#2 14. 10. 2010 11:21 — Editoval Rumburak (14. 10. 2010 11:24)
Re: Lokální extrém funkcí více proměnných
Podezřelými body jsou obecně
(1) body ležící v množnině 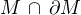 , kde
, kde  je množina, na níž extrém hledáme, a
je množina, na níž extrém hledáme, a  hranice této množiny,
hranice této množiny,
(2) ty vnitřní body množiny  , v nichž neexistuje některá parciální derivace funkce
, v nichž neexistuje některá parciální derivace funkce  ,
,
(3) ty vnitřní body množiny  , v nichž jsou všechny (zde obě) parciální derivace funkce
, v nichž jsou všechny (zde obě) parciální derivace funkce  rovny 0.
rovny 0.
V našem přípdě se uplatní pouze podmínka (2) pro bod [0, 0] - zde dokonce neexistuje ani jedna z obou PD .
Doplňující podmínka s druhými derivacemi má význam pouze v situaci (3).
Offline
#3 14. 10. 2010 13:21
- maly_kaja_hajnejch-Lazov
- Příspěvky: 467
- Reputace: 24
Re: Lokální extrém funkcí více proměnných
Vynikajici shrnuti, jenom bych doplnil, že v b) jsou podezřelé dokonce jenom ty vnitřní body množiny M, v nichž neexistuje některá parciální derivace funkce f a všechny derivace které existují jsou rovny nule.
Jinými slovy, bod, kde jedna derivace neexistuje a druha je treba 7 podezrely neni.
Offline
#4 14. 10. 2010 13:30 — Editoval Rumburak (15. 10. 2010 16:12)
Re: Lokální extrém funkcí více proměnných
↑ maly_kaja_hajnejch-Lazov:
Na toto upřesnění k podmínce (2) jsem si tentokrát nevzpomněl, děkuji :-).
Viz ↑↑ Rumburak: . Ale jak zjišťuji, tento odkaz NEFUNGUJE, netuším proč.
EDIT: Už vím, mělo se to udělat takto: Odkaz
Offline