Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 10. 04. 2008 17:25
Limity cos, sin
Zdravím všechny a opět se zde dovolávám pomoci respektive alespoň malého nakopnutí:-)
Zrovna řeším limity s sin a cos a vůbec si nevím rady, když tam jsou právě cosiny a siny...
příklady:
1)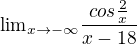
2)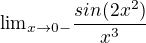
3)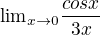
Opravdu nevím co s tím, snažil jsem se některé upravit na vzorec, ale bohužel jsem neslavil úspěch.
A ještě k tomuto tématu by mě zajímalo zda  a
a 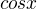 sami o sobě mají limitu??
sami o sobě mají limitu??
Díky za každou radu
Offline
#2 10. 04. 2008 18:05
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Limity cos, sin
↑ NetFenix:
Zdravim :-) zacnu od konce
- zkus si vybavit (nebo najit) graf sunx , cos x
- zkus si vybavit definici limity (muzes kazdeho typu - vlastni ve vlastnim bode, nevlastni ... ) a co z toho vyplyva? - ktery typ limit prichazi v uvahu pro tento typ funkci?
v zadani 1, 3, je potreba si uvedomit, cemu se rovna cos 0 (proc zrovna 0?)
v zadani 1 vsimat si znamenka podilu (jelikoz udavas, ze x se blizi k -oo) - takove to zname "minus" deleno "minus" ...
Zadani 2 se da upravit pomoci substituce na tvar 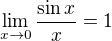 - prelozeno z rustiny je to "prvni pozoruhodna limita" - odpovidajici cesky vyznam jsem zatim nenasla :-)
- prelozeno z rustiny je to "prvni pozoruhodna limita" - odpovidajici cesky vyznam jsem zatim nenasla :-)
Tak se pripadne ozvi, jak to jde. OK?
Offline
#3 10. 04. 2008 18:10
Re: Limity cos, sin
Sakrys, jelena me predbehla...
Priklad 1:
Staci uvaha: Vyraz 2/x jde k 0, a tedy cos(x/2) jde k jedne, dal to urcite zvladnes sam.
Priklad 2:
Uprava na stadardni limitu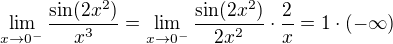
Priklad 3:
Podobne jako Priklad 1. Ale pozor, tahle limita neexistuje
Co se tyce toho, zda maji funkce sin a cos limitu, tak je dulezite, o limitu v jakem bode jde. Sin a cos maji limity ve vsech bodech krome oo a -oo
Nothing in the world that's worth having comes easy.
Always do what you are most afraid of.
Offline
#4 10. 04. 2008 18:21
Re: Limity cos, sin
No tak z grafu si myslím, že limita když platí že z definice |an-a|<epsilon pak by to mělo být že limita je rovna nule. Snad to říkám správně.
To zadání dvojky už mám ta substituce mě vůbec nenapadla.
Ale ta 1 a 3 vůbec nevim ani teď, :-(
Offline
#7 11. 04. 2008 10:04
Re: Limity cos, sin
Jeste poznamka k tomuhle: ↑ NetFenix:, neplet si definici limity funkce a limity posloupnosti, je to uplne neco jineho.
Nothing in the world that's worth having comes easy.
Always do what you are most afraid of.
Offline